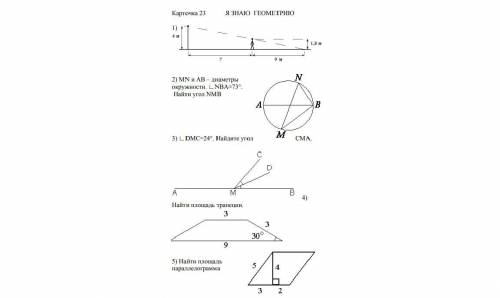
Задание по геометрии карточка я знаю геометрию 23 нужно полное решение
Популярные вопросы
- 1. Отметьте высказывания словом да , неправильные - словом «нет»А....
2 - Составь предложения к схемам. 1. О, _ _ _ _! 2. , О. 3. ,О!...
3 - 3. Периметр трикутника АВС, описаного навколо кола, дорівнює 24см....
2 - Где возникла жизнь (короче)...
2 - Основание пирамиды - равнобедренный треугольник с углом 120градусов...
3 - Н. заболоцкого вечер на оке Рифма стиха (парная, перекрестная, опоясывающая)....
3 - Сложите диалог в ресторане на английском языке на 6-7 реплик ...
2 - решить (можно ещё немного с объяснением...
2 - Знайти ,прочитати й презентувати (у будь -якій формі гуморески П.Глазового...
1 - Распределите указанных животных по наиболее часто переносимым ими болезням:ёжмышьлисасвиньякошкакрыса@чумакишечные...
2
ответ:а) -58 градусов б) 56 градусов в) 42 градусов
На картинке мы видим треугольник ABC. Правильно запишем условия задания, чтобы ничего не упустить:
Нам известно, что угол А равен 90 градусов, угол C равен 40 градусов, и сторона АС равна 8 сантиметров. Мы должны найти длину стороны ВС.
Для начала вспомним, как выглядит сумма углов треугольника. В треугольнике сумма всех углов всегда равна 180 градусов. Зная, что угол А равен 90 градусов и угол C равен 40 градусов, мы можем найти третий угол треугольника:
Угол B = 180 - угол А - угол C = 180 - 90 - 40 = 50 градусов.
Теперь, используя теорему синусов, мы можем найти сторону ВС. Теорема синусов гласит:
a/sin(A) = c/sin(C)
Где a, A - сторона и противолежащий ей угол, а c, C - сторона и противолежащий ей угол.
Применим теорему синусов к нашей задаче:
8/sin(50) = ВС/sin(40)
Теперь решим это уравнение, найдя ВС:
ВС * sin(50) = 8 * sin(40)
ВС = (8 * sin(40))/sin(50)
Подставляем числа в уравнение:
ВС ≈ (8 * 0.64278761)/0.76604444 ≈ 6.7549
Таким образом, длина стороны ВС примерно равна 6.7549 сантиметров.
Теперь наш ответ:
Длина стороны ВС составляет около 6.7549 сантиметров.