Задание по геометрии: 1) В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.
2) Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Мне нужно написать мини сочинение на тему несклоняемые имена существительные на...
3 - Нужно написать свое продолжение. вы мне хотя бы по напишите, я смогу перевести....
1 - Сочинение-рассуждение написать сочинение-рассуждение на тему почему гагин назвал...
3 - Сочинение на тему птицы говорят нам...
3 - Вданной действительной квадратной матрице порядка n найти сумму элементов строки,...
1 - Расставьте коэффициенты преобразовав схемы в уравнения реакций o2+p=p2o5 n2+li=li3n...
1 - Какая масса соли образуется при взаимодействии цинка с раствором серной кислоты...
2 - Мосты,осенний,ветер,ненастный,канавка,.праздник,шутка,поздно,столовая,участвовать,медовый,зимовать,письмо...
2 - Верно ли утверждение: 1) наименьшее составное нечетное число - 15 2) число, оканчевающиеся...
1 - 1) h2so4+so3-- h2s2o7 2) 2cr(oh)3+3h2so4-- cr2(so4)3+6h2o 3) na2co3+h2so4-- h2o+co2+na2so4...
3
Чертежи смотрите во вложении.
✧Задание №1.✧
В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.
Дано :
ΔАВС - равнобедренный и прямоугольный (∠В = 90°, АВ = СВ).
АС = 12 см.
Найти :
АВ = ?
СВ = ?
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).Пусть АВ = СВ = х. Тогда АВ² + СВ² = АС²
х² + х² = 12²
2х² = 144
х² = 72
х₁ =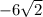 - не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.
- не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.
х₂ =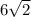 - подходит.
- подходит.
Тогда АВ = СВ = х =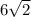 см.
см.
✧Задание №2.✧
Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.
Дано :
Четырёхугольник ABCD - ромб.
ВС = 13 см, АС = 24 см.
Найти :
BD = ?
В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны.Следовательно, АС⊥BD, ВО =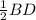 , CO =
, CO = 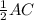 =
= 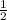 *24 см = 12 см.
*24 см = 12 см.
Рассмотрим ΔВОС - прямоугольный (∠ВОС = 90°).
По теореме Пифагора -
ВО² + СО² = ВС²
ВО² = ВС² - СО² = 13² - 12² = 169 - 144 = 25 ⇒ ВО =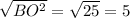 см.
см.
Тогда BD = 2*BO = 2*5 см = 10 см.
10 см.