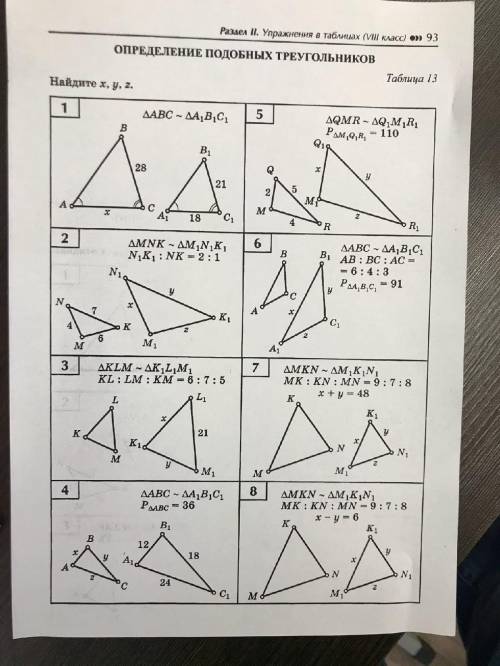
Задачи на определение подобных треугольников. задачи номер 4 и 5
Другие вопросы по теме Геометрия
Популярные вопросы
- Определи формулу линейной функции, график которой параллелен...
2 - Задание 1. Письменно. Какое значение имеет наука систематика...
3 - Помгите пх,тут якобы надо поставить + или -*+ это верно -это...
2 - Выясните, в каком отношении находится каждая пара множеств: а)...
3 - ПочемуСреднюю Сибирь можно назвать алмазно-золотоносной кладовой...
3 - ть, будь ласка( Порівняйте гуморальну і нервову ругуляцію, із...
2 - с этим заданием. Плачу не много балов, но мне оч нужен ответ,...
1 - Яку корисну роботу виконує трактор вагою 10kH при підйомі на...
3 - Что ты можешь сказать о поведении младшей дочки, она была......
3 - У выражение: а)-3а⁵·4ав⁶ б)(-2ху⁶)⁴ в)(-3а³у⁴)³...
2
В данной задаче изображены два треугольника - ABC и DEF.
Нам нужно определить, являются ли треугольники подобными.
Для этого мы должны сравнить соответствующие стороны треугольников и соотношения между ними.
Стороны треугольника ABC:
AB = 5 см
BC = 7 см
CA = 8 см
Стороны треугольника DEF:
DE = 2 см
EF = 2.8 см
FD = 3.2 см
Чтобы определить, являются ли треугольники подобными, мы должны сравнить соотношение длин сторон. Если соотношение сторон одного треугольника равно соотношению сторон другого треугольника, то треугольники подобны.
4) Давайте сравним соотношения сторон треугольников ABC и DEF:
AB/DE = 5/2 = 2.5
BC/EF = 7/2.8 = 2.5
CA/FD = 8/3.2 = 2.5
В данном случае все соотношения равны 2.5, поэтому мы можем сделать вывод, что треугольники ABC и DEF подобны.
Задача номер 5:
В данной задаче изображены два треугольника - ABC и DEF.
Нам нужно определить, являются ли треугольники подобными.
Для этого мы должны сравнить соответствующие стороны треугольников и соотношения между ними.
Стороны треугольника ABC:
AB = 8 см
BC = 12 см
CA = 16 см
Стороны треугольника DEF:
DE = 10 см
EF = 15 см
FD = 20 см
5) Давайте сравним соотношения сторон треугольников ABC и DEF:
AB/DE = 8/10 = 0.8
BC/EF = 12/15 = 0.8
CA/FD = 16/20 = 0.8
В данном случае все соотношения равны 0.8, поэтому мы можем сделать вывод, что треугольники ABC и DEF подобны.
Для подобных треугольников соотношение длин сторон будет одинаковым, и мы видим, что в обоих задачах соотношение равно, поэтому можем утверждать, что треугольники подобны.