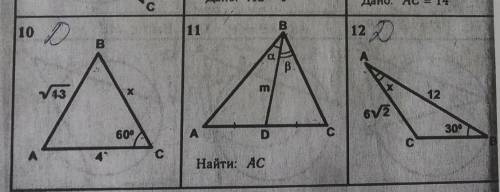
задачи и упражнения на готовых чертежах таблица 9.6 решение треугольников Найти X. задачи 9 и 12.​

Для решения задачи, представленной на рисунке, нам необходимо применить знания о сумме углов треугольника и о соотношении длин сторон в прямоугольном треугольнике.

Задача 9:
В данной задаче требуется найти значение угла X.

Обратимся к углу Y. На чертеже видно, что угол Y образован горизонтальной линией, которая является нижней основной стороной треугольника, и одной из диагоналей таблицы. Из этого можно сделать вывод, что угол Y является прямым углом (90°).

Таким образом, мы можем записать:
м_угл_Y + м_угл_B + м_угл_X = 180°.

Подставляя известные значения, получаем:
90° + 51° + м_угл_X = 180°.

Для нахождения значений угла X нам нужно решить следующее уравнение:
90° + 51° + м_угл_X = 180°.

Сокращаем выражение:
141° + м_угл_X = 180°.

Получаем:
м_угл_X = 180° - 141°.

Вычисляем:
м_угл_X = 39°.

Ответ: угол X равен 39°.

Задача 12:
В данной задаче требуется найти значения длин сторон AC и BC прямоугольного треугольника.

На чертеже видно, что сторона СА является одним из катетов этого треугольника, а сторона ВС является гипотенузой. Мы знаем, что длина гипотенузы в прямоугольном треугольнике равна квадратному корню из суммы квадратов длин катетов.

Таким образом, мы можем записать:
AC^2 + BC^2 = AB^2.

Подставляя известные значения, получаем:
14^2 + AC^2 = 10^2.

Вычисляем:
196 + AC^2 = 100.

Переносим "196" в другую сторону уравнения:
AC^2 = 100 - 196.

Вычисляем:
AC^2 = -96.

Поскольку получили отрицательное число, это означает, что треугольник не существует.

Ответ: треугольник с заданными сторонами не существует.