У коло вписано чотирикутник ABCD. Кут А в 3 рази більший за кут С, а кут В у 5 разів менший від кута А. Знайдіть кут D.

В окружность вписан четырехугольник ABCD. Угол А в 3 раза больше угла С, а угол В в 5 раз меньше угла А. Найдите угол D.

Объяснение:

Пусть ∠С=х°,  тогда ∠А=3х°, а ∠В=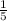 *∠А.

Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° : ∠А+∠С=180°

х+3х=180 , х=45°.

∠А=45°*3  ⇒ ∠В =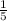 *(45*3)=27° .

Т.к  ∠В+∠D=180° , то ∠D=180°--27°=153°

Якщо чотирикутник можна вписати у коло, то сума його протилежних кутів становить 180°.

Нехай ∠С=х°, тоді ∠А=3х°, ∠В=(3х/5)°, тоді

х+3х=180;  4х=180;  х=45;  ∠С=45°,  ∠А=45*3=135°

∠В=3*45:5=27°

∠В+∠D=180°; ∠D=180-27=153°

Відповідь: 153°