задача:
в трапеции PKMN боковая сторона PK перпендикулярна основанию KM. окружность проходит через точки M и N и
касается стороны PK в точке O
вопрос: Найти расстояние от точки O до прямой MN если PN=11; KM=5
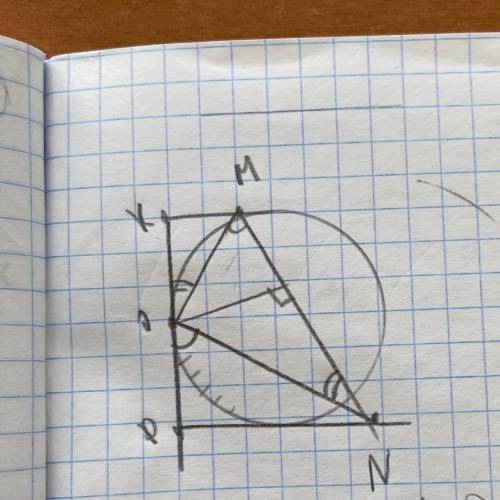
Другие вопросы по теме Геометрия
Популярные вопросы
- Выразите 1 мин 48 сек в минутах и запишите это в виде десятичной дроби....
2 - №1 у морских свинок черный цвет доминирует над белым. какое потомство...
1 - Решите уравнение : 4х(х+50)=20х -х^2...
3 - Расстояние между двумя 900 километров. два поезда вышли из этих городов...
1 - Составить рассказ про какой нибудь случай и план...
2 - Что такое пищеварение каково значение этого процесса для питания человека....
3 - Составьте формулу соли-нитрата цинка...
3 - Объем газообразного оксида азота(ii) составляет 3,36 литров. вычислите...
1 - Впиши в пропуски is, isn t, are или aren,t. 1. jenny isn t, a student....
3 - Втреугольнике abc угол c равен 90 ,угол b равен 60,bc равен 2,5.найти...
1
OH - перпендикуляр к прямой MN.
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой.
Угол KOM = дугаОМ/2. (Угол KOM образован касательной и хордой, проходящей через точку касания.)
Вписанный угол измеряется половиной дуги, на которую он опирается.
Угол ONM = дугаОМ/2 = угол KOM.
Аналогично: уголPON = дугаON = уголOMN.
Треугольники OKM и NHO подобны: KM/OH=OM/ON.
Из подобия треугольников MHO и OPN: OM/ON=OH/PN.
KM/OH=OM/ON=OH/PN, KM/OH=OH/PN, OH^2=KM*PN, OH=√56*14=28.