з точки до прямої проведено перпендикуляр і похилу, довжина якої 12 см. Знайдіть довжину перпендикуляра та проекції похилої, якщо похила утворює

Question

Геометрия: з точки до прямої проведено перпендикуляр і похилу, довжина якої 12 см. Знайдіть довжину перпендикуляра та проекції похилої, якщо похила утворює з прямою кут 30°​

shshdbAsan · Answer

Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.

Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.

Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы

А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.

Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: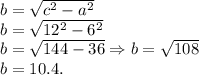 $b = \sqrt{c^2-a^2}\\b = \sqrt{12^2-6^2}\\b = \sqrt{144-36} \Rightarrow b = \sqrt{108}\\b = 10.4.$

Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).

з точки до прямої проведено перпендикуляр і похилу, довжина якої 12 см. Знайдіть довжину перпендикуляра та проекції похилої, якщо похила утворює з прямою кут 30°​

Популярные вопросы

з точки до прямої проведено перпендикуляр і похилу, довжина якої 12 см. Знайдіть довжину перпендикуляра та проекції похилої, якщо похила утворює з прямою кут 30°