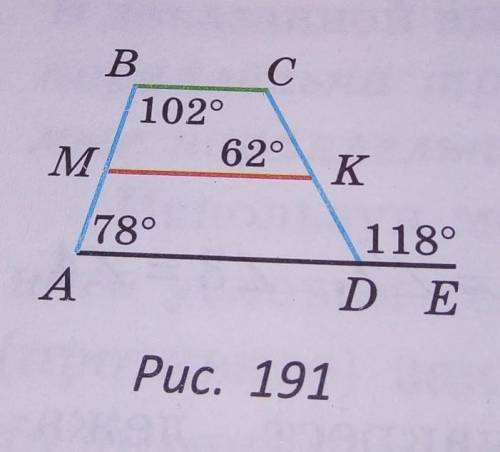
Выясните, пересекутся ли при продолжении отрезки MK и BC (рис. 191) Если ответите не по теме или просто ради балов, отмечу нарушение)))
Другие вопросы по теме Геометрия
Популярные вопросы
- Впаскале составьте программу вывода на экран таблицы степеней 3n, где 0 ≤ n ≤...
2 - 55 5 5 = 16 расставить нужные знаки...
1 - Написать мини-сочинение на тему кристальный день , либо на тему прощание с летом...
1 - Фразеологизмы. примеры фразеологизмов к словам: 1)язык 2)водить 3)заря 4)слово...
3 - 1: 5/9 подробное решение если можно...
2 - Причины и последствия появления антанты и тройственного союза...
1 - Скакими веществами взаимодействует и глюкоза, и фруктоза?...
1 - Как определить численность майского жука в минске? ?...
3 - Спишіть, розставляючи розділові знаки.. увечері при заході сонця небо бралося...
1 - Всаду поселились 4 пары скворьцов.у каждой пары 6 птенцов.сколько всего скворьцов...
1
Не пересекаться, т. К мк средняя линия трапеции
ответ: нет не пересекутся
Объяснение:
Потому что они являются параллельными прямыми.
Начнем с того, что у нас есть две пары параллельных прямых: AB || CD и AC || BD. Это значит, что углы BAC и ADC являются соответственными углами, а также углы ABC и ACD являются соответственными углами.
Посмотрим на угол ABC. Поскольку углы ABC и ACD являются соответственными углами, они равны друг другу.
Теперь обратимся к углу BAC. Поскольку BD || AC, угол BAC и угол BCD являются соответственными углами и должны быть равны.
Итак, у нас есть два равных угла: угол ABC и угол BAC. При продолжении отрезка MK он будет проходить через точку C, и отрезок BC будет продолжен до точки K.
Таким образом, отрезки MK и BC пересекутся при их продолжении в точке K.
Обоснование: Мы использовали свойство параллельных прямых и соответственные углы для доказательства пересечения отрезков MK и BC при их продолжении. Также мы используем базовые свойства углов и параллельных линий, которые были доказаны ранее.
Шаги решения:
1. Заметьте, что AB || CD и AC || BD.
2. Используйте свойство соответственных углов, чтобы найти углы, которые равны: угол ABC и угол ACD, угол BAC и угол BCD.
3. Заключите, что отрезки MK и BC пересекаются при их продолжении в точке K на рисунке.
Надеюсь, эта информация будет полезной и понятной для школьника.