Вычислить угол между векторами? буду : *: * вычислите угол между векторами: а) вектор a (2; -2; 0) и вектор b (3; 0; -3) б) вектор a (0; 5; 0) и вектор b (0; -корень из 3; 1) в) вектор а (-2; 5; 2; 5; 0) и вектор b (-5; 5; 5; корень из 2)

cos(a,b,c)=(x1x2+y1y2+z1z2)/sqrt(x1^2+y1^2+z1^2)*sqrt(x2^2+y2^2+z2^2)

а)cos(a,b,c)=(6+0+0)/sqrt(4+4+0)*sqrt(9+0+9)=6/2sqrt(2)*3sqrt(2)=6/12=1/2

cos(a,b,c)=60*

б)cos(a,b,c)=0+(-5sqrt(3))+0/sqrt(0+25+0)*sqrt(0+3+1)=-5sqrt(3)/10=-sqrt(3)/2

cos(a,b,c)=150*

в) тут ты допустил опечатку исправь не может быть в векторе а пять координат, а в б четыре

Дальше стрелочку на векторами писать не буду, не знаю, как правильно. 

а) Находим скалярное произведение:

ab=2·3+(-2)·0+0·(-3)=6

Находим абсолютные величины:

|a|=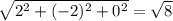 

|b|=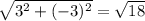 

Находим косинус угла:

cos α =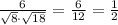  

α=60° 

б) Находим скалярное произведение:

ab=0·0+5·(-√3)+0·1=-5√3

Находим абсолютные величины:

|a|=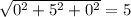 

|b|=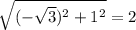 

Находим косинус угла:

cos α =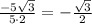  

α=150°

в) Находим скалярное произведение:

ab=-2,5·(-5)+2,5·5,5=12,5+13,75=26,25

Находим абсолютные величины:

|a|=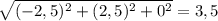 

|b|=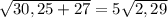 

Находим косинус угла:

cos α =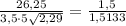  ≈ 0,9912

α≈7°