вычислить площадь криволинейной трапеции, ограниченной линиями
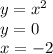
Другие вопросы по теме Геометрия
Популярные вопросы
- Выбери верную формулу перевода 8 Гбайт в биты: * 8*8 битов8*1024*1024*8 битов8*1024*8...
2 - Мына сөздерді орфаглафиялық нормаға сәйкестендір...
2 - 79. Атооч жөндөмөсүндөгү сөздөр менен айкашуучу жандоочторду тапкыла.а) жана...
3 - План сложный по Революции в Недерлаландах...
3 - Егер a=132 ал b саны a дан 25 ке кем болса а -b өрнегінің менін есепте...
3 - Упрастите выражение а^2+4а/а^2+5а+16 и найдите его значение при а=-2 2.упростите...
2 - Раскройте скоюки: She (to be) painter.They already (have ,to be). He (to...
2 - европейские революции 1848-49 гг таблица государства австровенгрия, Германия,...
1 - ответить на вопросы: 1. Как называется мусульманский храм?2. Укажите общие...
3 - Плата за квартиру, в которой проживает семья Серёжи на протяжении двух лет,...
1
y = x² - парабола ветвями вверх с вершиной в начале координат.
y = 0 - прямая, параллельная оси OX.
Пределы интегрирования - точки пересечения графиков:
x² = 0 ⇒ x = 0
Тогда площадь криволинейной трапеции будет так:
S = (0)∫(-2) x²dx = ∫x²dx = x³/3 |⁰₋₂ = 0³/3 - (-2)³/3 = 0 - (-8/3) = 0 + 8/3 = 8/3 кв. ед.
ответ: S = 8/3 кв. ед.