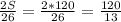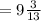Втреугольнике со сторонами 10см,24см и 26см найдите высоту, опущенную на большую сторону
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Найдите отношения: 18:6 9:5 133: 19245252. Найти отношения...
1 - What makes a happy family? 12-15 предложений...
1 - Природа - летопись Какую бы часть земли вы ни взяли, везде географические...
1 - Быстрова 8 класс упражнение 14 задание 2...
1 - Конспект жанры классической литературы XIX века ...
3 - сочинение от имени путешественника от 1-го лица. направление...
2 - ЗСП-2 Вооружи (ться— разоружение, подогревать), престарелый),поглота...
2 - дать краткую характеристику 3 соседям римской империи...
1 - Составить рассказ 7-8 предложений по пословице на тему: Язык,...
2 - Лабораторная работа №1 Классификация тканей растений Цель: знакомство...
2
Найдем площадь данного треугольника по формуле Герона
S=√(p(p-a)(p-b)(p-c)=√(30*20*6*4)=√14400=120 (см²)
Большая сторона а=26 см.
S=1\2 * a * h
120=1\2 * 26 * h
h=120\13=9 3\13 cм.
ответ: 9 3\13 см.
Высота треугольника равна частному от деления удвоенной площади треугольника на сторону, к которой она проведена.
Найдем площадь по формуле Герона: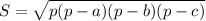
где р - полупериметр, р=(a+b+c)/2, a, b, c - стороны треугольника
р = (24+10+26)/2 = 30
S =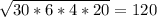
Найдем высоту:
h =