Втреугольнике abc проведены биссектрисы из вершин a и b. точка их пересечения обозначена d. найдите угол adb, если: 1) угол а=50(градусам), угол в=100(градусам). 2) угол а=а, угол в=в; 3) угол с=130; 4) угол с=у
Другие вопросы по теме Геометрия
Популярные вопросы
- Write down the correct forms of the verbs to complete the sentences...
2 - Постоянно путаюсь по типам данных. запишите для каждой переменной...
3 - Пож найдите корень у слова безветренный...
3 - Кавказский пленник : действия жили на и костылина ,2 побег...
2 - Найдите разность чисел: 7 3/14 - 4 1/7 +15 заранее...
3 - Решить на с++ дано натуральное число nn. требуется найти его разложение...
3 - Найди и подчеркни служебные части речи. для ученья нет старости....
1 - Длина тур. тропы равна 55 км. за несколько дней туристы всего пути....
3 - 15. себеп бағыныңқы сабақтас сөйлемді табыңыз. а) мен оқыған кітап...
2 - Нужно придумать предложение со словом яркость...
3
Биссектриса делит угол пополам, т.е. ∠ABD = ∠DBC; ∠BAD=∠DAC.
1)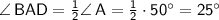
И рассмотрим треугольник ABD в нем сумма углов должна быть равна 180°,т.е.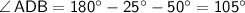
2) Аналогично с примером 1)
3) Сумма углов треугольника ABC равна 180°, т.е. ∠A+∠B+∠C=180°.
∠A + ∠B + 130° = 180°
∠A + ∠B = 180° - 130°
∠A + ∠B = 50°
∠ADB = 180° - 1/2(∠A + ∠B) = 180° - 1/2 * 50° = 180° - 25° = 155°
4) Аналогично с примером 3)
∠A + ∠B + ∠C = 180°
∠A + ∠B +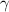 = 180°
= 180°
Тогда