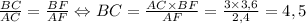1. Геометрия
  2. Втреугольнике аbc на сторонах

Втреугольнике аbc на сторонах ав и ас выбраны точки м и n так, что вм: ма=сn: na=1: 2. оказалось , что отрезок мn содержит центр окружности , вписанной в треугольник авс. найдите вс , если ав=6 ас=3.

hehehdhd hehehdhd    2   12.05.2019 19:07    7

Ответы
kapitan2001 kapitan2001  30.09.2020 17:38

4,5

Объяснение:

ПОКАЗАТЬ ОТВЕТЫ
yourbae yourbae  30.09.2020 17:38

Будем пользоваться теоремой о биссектрисе.

Она заключается в следующем: отношение сторон треугольника, содержащихся в угле, из которого проведена биссектриса, равна отношению отрезков, на которые делит биссектриса противолежащую сторону.

Назовем точку пересечения MN и биссектрисы AK через R; Тогда из данного в условии легко вывести, что биссектриса угла C проходит через R. Пусть RC ∩ AB = F; Пусть AM=2x, MB=x. Тогда x=2; По теореме Менелая для треугольника AMN: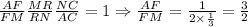 \frac{AF}{FM}\frac{MR}{RN}\frac{NC}{AC}=1 \Rightarrow \frac{AF}{FM} =\frac{1}{2\times\frac{1}{3} } =\frac{3}{2}, ну а отсюда легко получить AF=2,4 и FM=1,6; Значит BF=3,6 и AF=2,4; По вышеизложенной теореме о биссектрисе имеем: \frac{BC}{AC}= \frac{BF}{AF}\Leftrightarrow BC=\frac{AC\times BF}{AF}=\frac{3\times 3,6}{2,4}=4,5


Втреугольнике аbc на сторонах ав и ас выбраны точки м и n так, что вм: ма=сn: na=1: 2. оказалось , ч
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
YanaDovgik YanaDovgik  30.11.2020 18:08
аналитическая геометрия на плоскости Даны вершины треугольника А(11,-10), В(6,2), С(0,-6). Найти: а) уравнение стороны АВ. б) уравнение высоты СЯ. в) уравнение медианы AM. г)...
katyaydalova15 katyaydalova15  30.11.2020 18:08
Точка K лежит по один бік від обох паралельних площин a(альфа) i b(бета). Через точку K проведено дві прямі a і b, що перетина ють площину а(альфа) у точках A1 і A2, а площину...
ПоляКетчуп ПоляКетчуп  30.11.2020 18:08
Укажите, какие из утверждений являются истинными. Выберите все возможные варианты ответов. Укажите один или несколько правильных вариантов ответа: Средняя линия равнобедренного...
catxripunowa catxripunowa  30.11.2020 18:08
1. Дано прямі a і b, паралельні до прямої с. Яке взаємне розміщення прямих a і b? а) перетинаються; б) паралельні; в)мимобіжні. 2. Дано мимобіжні прямі a і b. Скільки існує площин,...
ДобрыйАндрей111 ДобрыйАндрей111  30.11.2020 18:08
с геометрией там 2 фотки, вторая в следующем вопросе (1/2)​...
mariamyp mariamyp  30.11.2020 18:08
аналитическая геометрия на плоскости Даны вершины треугольника А(11,-10), В(6,2), С(0,-6). Найти: а) уравнение стороны АВ. б) уравнение высоты СЯ. в) уравнение медианы AM. г)...
Sidoriva Sidoriva  01.11.2020 14:16
11.На рис.4 изображены подобные треугольни- КИ. Используя величины, данные на рисунке,найдите отношение площади большего треу-ГОЛЬНика КПлощади меньшего.А) 9:4;В) 3:2:C) 4:9;D)...
pdv20 pdv20  23.05.2020 13:25
Гiпотенуза AB прямокутного трикутника ABC є хордою кола радiуса 10.Вершина C лежить на дiаметрi кола, який паралельний до гiпотенузи.Кут CAB рiвний 75◦. Знайти площу трикутника...
DityaDyavola DityaDyavola  22.05.2020 12:35
Куты при більшій основі трапеции 60 і 30 градусив. Більша бічна сторона трапеції дорівнює 12 см а сума її основ 20 см. Знайдіть площу трапеції​...
Murew Murew  22.05.2020 23:08
Основой прямого паралепипеда является ромб с тупым углом 120 ° и большей диагональю 8√3 см. меньшая диагональ паралепипеда образует с его высотой угол 45 ° зн площадь боковой...

Популярные вопросы