Втреугольнике abc ab=15м, ac=20м, bc=32м.на стороне ab отложен отрезок ad=9м,т а на стороне ac - отрезок ae=12м.найдите de и отношение площадей треугольников abc и ade.

Ответы

Lqoki11 06.06.2020 21:59

Рассмотрим треугольники ABC и ADE. Угол А - общий для этих треугольников, а две пары сторон, между которыми заключён угол А, пропорциональны:

$\frac{AB}{AD}=\frac{15}{9}=\frac{5}{3}$

$\frac{AC}{AE}=\frac{20}{12}=\frac{5}{3}$

Следовательно, треугольники ABC и ADE подобны, коэффициент подобия равен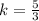 $k=\frac{5}{3}$ .

$DE=BC:k=32:\frac{5}{3}=\frac{96}{5}=19,2$ (м)

Отношение площадей подобных фигур равно квадрату коэффициента подобия:

$\frac{S(ABC)}{S(ADE)}=k^2=(\frac{5}{3})^2=\frac{25}{9}=2\frac{7}{9}$

ответ: DE=19,2 м; отношение площадей треугольников ABC и ADE равно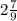 $2\frac{7}{9}$ .

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

333Хашимото3Ня333 12.04.2020 14:55

Lososepotam 12.04.2020 14:55

rainbiwcat750KO 12.04.2020 14:50

Nastya32q 12.04.2020 14:50

ravil863 04.03.2019 00:10

евген115 04.03.2019 00:10

ivan111111 04.03.2019 00:10

svatoslavsasko3 04.03.2019 00:10

лауракот 04.03.2019 00:10

Nasti12 12.05.2020 10:23