Вправильной треугольной призме авса1в1с1 сторона основания ав=10, а боковое ребро аа1=√(69). найдите расстояние от точки а до прямой вс1.
Ответы
Рисуем призму: нижнее основание АВС, верхнее - А1В1С1. Проведем в плоскостях АА1С1С и СС1В1В диагонали АС1 и ВС1 соответственно. Рассмотрим треуг-к АВС1. Искомое расстояние будет равно длине высоты, опущенной из А к ВС1(обоз-м ч\з АО). АС1=ВС1=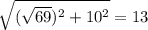 . В тр-ке АВС1 применим тер-му кос-в: 169=169 -100 - 2*13*10*cosABC1 => cosABC1=5/13 => sinABC1=
. В тр-ке АВС1 применим тер-му кос-в: 169=169 -100 - 2*13*10*cosABC1 => cosABC1=5/13 => sinABC1=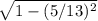 =12/13, а в тр-ке АВО sinABC1=sinABO=АО/АВ => AO=10*12/13= 120/13.
=12/13, а в тр-ке АВО sinABC1=sinABO=АО/АВ => AO=10*12/13= 120/13.
ПОКАЗАТЬ ОТВЕТЫ
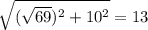 . В тр-ке АВС1 применим тер-му кос-в: 169=169 -100 - 2*13*10*cosABC1 => cosABC1=5/13 => sinABC1=
. В тр-ке АВС1 применим тер-му кос-в: 169=169 -100 - 2*13*10*cosABC1 => cosABC1=5/13 => sinABC1=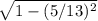 =12/13, а в тр-ке АВО sinABC1=sinABO=АО/АВ => AO=10*12/13= 120/13.
=12/13, а в тр-ке АВО sinABC1=sinABO=АО/АВ => AO=10*12/13= 120/13.
Другие вопросы по теме Геометрия
Популярные вопросы
- Добрий день, с сочинением по на тему - my autumn holiday...
1 - С.ю. витте основная роль в россии? (...
3 - От туристского лагеря до города 84 км. турист ехал на велосипеде из лагеря...
1 - Найдите значения выражения: 1)5a+5b если a+b=28 2)2c-6d если c-3d=25...
2 - K- k²o - koh- kno³ цифры снизу k koh соедены стрелками и k²o kno³ тоже...
2 - Задайте с ответами на пословицы и поговорки на числа 4 и 8...
2 - Задайте формулой линейную функцию график которой параллелен графику прямой...
1 - Вдвух мешка умещается 24кг картошки. сколько кг картошки умещается в...
2 - Площадь прямоугольника равна 36 см в квадрате, а его периметр 24 см....
3 - Сколько анионов можно получить при полной диссоциации (nh4)3p04?...
2