В треугольнике MKP дано: MK=
см,угол P=45°,угол M=60°.
Вычислите длину стороны KP.
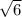
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить систему x+y 3 x-y больше или равно 1 надоо))...
1 - Растровый графический файл содержит цветное изображение с 64-ю...
3 - Запиши слова в два столбика: в первый – однокоренные слова, во...
3 - По задали наблюдать темпиратуру неделю и составить с ней диаграмму...
3 - Произведение чисел 9485 и 9 уменьшенное на их разницу...
1 - Переведите текст, ! , либо мне плохо listen to the text, then...
2 - Раньше при остановке сердца человек считался безоговорочно мертвым,...
3 - Решить уравнения 2 класса. х-9=4,у+7=15,35-х=30 с проверкой...
1 - На столе лежат красные и зелёные карандаши. их количество находится...
3 - Как правильно пишется отгнать или отогнать...
3
Дано, что угол P равен 45° и угол M равен 60°. Из этого можно сделать вывод, что третий угол треугольника MKP равен 180° - 45° - 60° = 75°.
Теперь нам нужно вычислить длину стороны KP. Для этого мы можем использовать теорему синусов, которая говорит, что отношение любой стороны треугольника к синусу её противолежащего угла равно отношению другой стороны к синусу её противолежащего угла.
В нашем случае, мы знаем длину стороны MK равную √6 см и угол M равный 60°.
Применяя теорему синусов, мы получаем:
MK / sin(M) = KP / sin(P)
√6 / sin(60°) = KP / sin(45°)
Мы можем выразить KP, переставив значения:
KP = (√6 / sin(60°)) * sin(45°)
Для решения этого уравнения, нам понадобятся значения синуса 60° и синуса 45°. Мы можем использовать таблицу значений тригонометрических функций или калькулятор.
sin(60°) = √3 / 2,
sin(45°) = 1 / √2
Подставляя эти значения в уравнение:
KP = (√6 / √3 / 2) * (1 / √2)
= √6 / √3 / √2
= (√6 / √6) * (√2 / √2)
= (√6 * √2) / √6
= √12 / √6
Мы можем упростить эту дробь, выделив общий множитель:
KP = (√(2 * 2 * 3)) / (√(2 * 3))
= (2√3) / √(2 * 3)
= (2√3) / √6.
Таким образом, длина стороны KP равна (2√3) / √6 см.