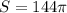Вокруг цилиндра с высотой 6 см описан шар,отрезок который соединяет центр этого шара с точкой круга основы цилиндра,образует с осью цилиндра угол 60 градусов.найти площадь поверхности шара

Сделаем схематический рисунок шара и цилиндра в нём.

Центр шара О,

Отрезок ОА=R и соединяет с центром шара О точку А на круге основы цилиндра.

Диаметр оснований цилиндра АВ, образующая ВС, ось цилиндра МН=ВС.

ОН = половина высоты цилиндра и равна 3 см.

Так как радиус шара образует с осью цилиндра угол 60º, то с диаметром цилиндра он

 образует угол 30º

АО=ОН:sin (30º)=3:0,5=6 см

R=6 см

Sсферы= 4πr²=4π6²= 144 см²

------------------------- 

-------------------------------------------------------------------------------------------------------------------------------

Для случая, когда радиус образует угол 60º не с осью цилиндра. а с его диаметром,

будет другой ответ, но ход решения, конечно, тот же. 

АО=ОН:sin (60º)=3*2:√3=3*2√3:√3√3=2√3

R=2√3 см

Sсферы= 4πr²=4π(2√3)²=4π12=48π см²

Так как в шар вписан цилиндр, тогда центр шара будет делить высоту цилиндра пополам, как показано на рисунке.

Исходя из прямоугольного треугольника на рисунке, найдем длину гипотенузы численно равной радиусу сферы:

Получаем R=6

Тогда площадь поверхности шара будет равна:

ответ: