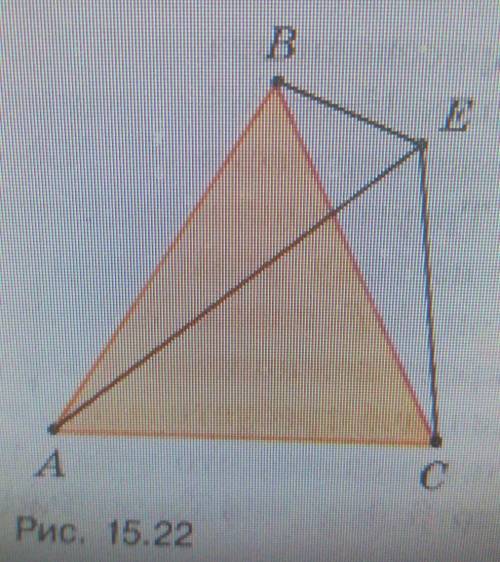
Вне равноктороннего тренуольника АBC
взята точка E так, что угл ВЕС равен 120°.
доажите, что ВЕ + C = AE (рис15.22). ​

Для доказательства ВЕ + C = AE, нам понадобится использовать несколько геометрических свойств и фактов о треугольниках.

1. В треугольнике АВС угол ВАС является внешним углом треугольника в отношении угла ВСЕ.
Согласно свойству внешних углов треугольника, угол ВАС равен сумме углов СВЕ и ВСЕ (угол ВАС = угол СВЕ + угол ВСЕ).
Рисунок:
A
/ \
/ \
/ \
B ----- C

2. Поскольку треугольник АВС - равнокорный, углы ВАC и АСВ также равны.
Следовательно, угол ВАС равен двукратному углу ВАС и двукратному углу СВЕ.
Угол ВАС = 2 * угол ВАС и угол ВАС = 2 * угол СВЕ.

3. Зная, что угол СВЕ равен 120°, мы можем записать следующее:
угол ВАС = 2 * угол СВЕ
2 * 120° = угол ВАС
240° = угол ВАС

Теперь мы можем продолжить с доказательством ВЕ + C = AE:

4. Рассмотрим треугольник ABE:
ВE + угол ВЕС + угол ВАС равны 180° (сумма углов треугольника).

5. Заметим, что угол ВАС равен сумме углов СВЕ и ВЕС:
угол ВАС = угол ВЕС + угол СВЕ
240° = угол ВЕС + 120°
240° - 120° = угол ВЕС
120° = угол ВЕС

6. Мы знаем, что угол ВЕС равен 120°, поэтому мы можем записать следующее:
ВE + 120° + 120° = 180°
ВE + 240° = 180°
ВE = 180° - 240°
ВE = -60°

7. Мы получили, что длина ВЕ равна -60°. Однако, поскольку это отрицательная длина, она должна быть изменена на противоположную сторону.
ВЕ = 60°

8. Из-за того, что треугольник равнокорный (сторона ВС равна стороне СА), мы можем использовать факт, что соответствующие стороны равностороннего треугольника равны.
Таким образом, ВЕ = С.

9. Значит, мы можем переписать равенство ВЕ + C = AE в следующем виде:
С + C = AE
2C = AE

Доказано, что ВЕ + C = AE.