Висота рівнобедриного трикутника проведена до основи дорівнює 8 см а радіус описаного навколо нього кола 13см знайти бічну сторону трикутника

Ответы

Søphia 01.10.2020 07:50

Дан равнобедренный треугольник АВС с высотой ВН = 8 см.

Радиус описанной окружности равен R = 13 см.

Пусть сторона АВ=ВС=а, а основание АС=b.

$R = \frac{a^{2}}{\sqrt{(2a)^{2}-b^{2}}} \\$

Рассмотрим треугольник АНВ - прямоугольный.

AB^2 = BH^2 + AH^2 или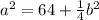 $a^{2} = 64 + \frac{1}{4}b^{2}$

Подставим в формулу для радиуса.

$13 = \frac{64+\frac{1}{4}b^{2}}{\sqrt{(2\sqrt{64+\frac{1}{4}b^{2}})^{2}}-b^{2}} \\ 13 = \frac{64+\frac{1}{4}b^{2}}{16} \\ 64 + \frac{1}{4}b^{2} = 13*16 \\ b=24$

AC = 24, следовательно, АН = 12.

АВ^2 = AH^2 + BH^2

$AB = \sqrt{208} = 4\sqrt{13}$

Висота рівнобедриного трикутника проведена до основи дорівнює 8 см а радіус описаного навколо нього

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

killpvpglava 31.03.2020 13:29

Одна из основ трапеции на 8 сантиметров короче другой, площадь равна 80 сантиметров, а высота 5 сантиметров. найти большую из основ трапеции...

grigorijperever 31.03.2020 13:29

В трикутнику АВС до сторони ВС проведено висоту АМ. Запишіть , як обчислити площу трикутника....

bintcliffe 31.03.2020 13:29

Ребята решить геометрию. ООчень нужно! Площа рівнобедреної трапеції дорівнює 24 см2, а її висота — 3 см. Знайдіть периметр трапеції, якщо її більша основа дорівнює 12 см....

chikurovden 31.03.2020 13:29

Задание #7Во Выберите предложение, в котором ввиду входит в состав союза. Выберите один из 4 вариантов ответа:1) Ввиду того, что завтра мы должны были сняться с якоря, было приказано...

LordКавайность 31.03.2020 13:29

Найдите градусную меру угла N треугольника MNK,если известно,что MN=NK,MK меньше NK ,а один из углов треугольника равен 70°....

Lisica99 31.03.2020 13:29

решить все выделенные задачи...

znayushiy18 31.03.2020 13:29

Найдите площадь равнобедренной трапеции с углом между диагоналями 120 и высотой 3...

ulyanagrab333 31.03.2020 13:28

Знайдіть модуль вектора a(-8;-2)...

Ангелина75645674 06.04.2019 08:25

Сделайте чертежи к ! 1)из точек c и d ,лежащих на одной из сторон данного острого угла, проведены перпендикуляры к этой стороне , пересекающие вторую сторону угла в точках a...

TheEasyCloud 06.04.2019 08:29

Дан прямоугольный параллелепипед abcda1b1c1d1. ортогональной проекцией a1c на плоскость b1bc является: a)b1cb)b1c1докажите. с ...

Висота рівнобедриного трикутника проведена до основи дорівнює 8 см а радіус описаного навколо нього кола 13см знайти бічну сторону трикутника

Популярные вопросы