Висота опущено на гіпотенузу прямокутного трикутника ділить її на відрізки 6 см і 18 см.Знайдіть сторони цього трикутника і висоту,проведену до гіпотенузи
Другие вопросы по теме Геометрия
Популярные вопросы
- 1.Жазушы Дүкенбай Досжанның қандай романы бар? 2.Жазушының «Жібек...
1 - 7-тапсырма. Б. Мәтіннен салт және сабақты етістерді тауып, тоғызқұмалақ...
1 - Практическая работа Экономические ресурсы ПРАКТИЧЕСКАЯ РАБОТА...
2 - Визначте валентності хімічних елементів, і позначте їх над знаками...
1 - Визначте кількість електронів і кількість нейтронів у атомі 31...
3 - Разложите на множители:1) 9х2-6ху+у2= 2) 25в2+10ав+а2=3) 4р2-4ар+а2...
1 - Нет у нас никого, равного ему в доблести - сочинение...
3 - Вася может вскопать огород за 12 часов, а Миша – в полтора раза...
1 - 3 Put the verbs into the past continuous. 1 I(ride) my bike when...
2 - Укажите количество местоимений во 2-м абзаце текста и да нормально...
2
Дано:
abc — прямокутний трикутник;a, b — катети, c — гіпотенуза h — висота, проведена до гіпотенузиaЗнайти:
a, b, h — ?Розв'язок:
1) Висота, проведена до гіпотенузи, є середнім пропорційним між проекцією катетів на гіпотенузу:
2)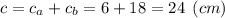
3) Катет є середнім пропорційним між гіпотенузою та проекцією цього катета на гіпотенузу:
Відповідь:
a = 12 cm; b = 12√3 cm; h = 6√3 cm.