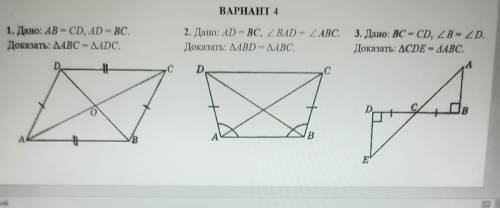
Вариант 4 1. Дано: = CD, AD - BC. Доказать: ДАВС - ДА DC.
2. Дано: AD - BC, - ДАВС. 3. Дано: CD, LB- LD. Доказать: AABD - ДАВС. Доказать: ACDE - AABC.

Добрый день! Давайте разберем по очереди каждое задание и найдем решение.

1. Дано: = CD, AD - BC. Доказать: ДАВС - ДА DC.

Нам дано, что CD равно, то есть CD = CD. И также дано, что AD - BC. Мы хотим доказать, что ДАВС - ДА DC.

Решение:
Для начала, у нас есть равенство CD = CD, это значит, что отрезки CD и CD равны друг другу по длине.

Теперь предположим, что ДАВС - ДА DC. Это означает, что у нас есть два угла, которые равны и две стороны, которые равны.

Давайте рассмотрим углы. У нас есть два вертикальных угла CDA и DСД, которые должны быть равны. Так как CD = CD, это значит, что угол CDA = угол DСД.

Теперь рассмотрим стороны. У нас есть стороны AD и DC. Из условия задачи мы знаем, что AD - BC. Но так как у нас есть равенство CD = CD, это значит, что сторона DC также равна AD.

Итак, мы доказали, что у нас есть два угла, которые равны и две стороны, которые равны. То есть, ДАВС - ДА DC.

2. Дано: AD - BC, - ДАВС.

Нам дано, что AD - BC и что угол ДАВС отрицательный.

Решение:
Мы знаем, что AD - BC, то есть сторона AD больше стороны BC.

Если у нас есть три стороны треугольника, то мы можем использовать неравенство треугольника. Согласно неравенству треугольника, сумма двух сторон треугольника должна быть больше третьей стороны.

Так как у нас есть AD > BC, это значит, что AC + CD больше, чем AD.

Теперь предположим, что у нас есть треугольник ACD. Мы знаем, что угол ДАВС отрицательный, это означает, что угол ACB больше, чем угол BCD.

Так как AC + CD больше, чем AD, а угол ACB больше, чем угол BCD, мы можем заключить, что ACD не может быть треугольником. То есть, ДАВС не может существовать.

3. Дано: CD, LB- LD. Доказать: AABD - ДАВС. Доказать: ACDE - AABC.

Нам дано, что CD и LB - LD. Мы хотим доказать, что AABD - ДАВС и ACDE - AABC.

Решение:
Давайте рассмотрим каждое доказательство по отдельности.

Доказательство AABD - ДАВС:
Мы знаем, что CD, это значит, что сторона CD существует.
Мы также знаем, что LB - LD. Это означает, что угол LBD больше, чем угол LDB.
Теперь рассмотрим стороны BD и AB. Мы знаем, что BD - AB. Если BD больше, чем AB, то угол BDA будет больше, чем угол BAD.
Также мы знаем, что у нас есть равенство CD = CD, это значит, что угол ACD равен углу CDA.
Итак, мы доказали, что у нас есть два угла, которые равны и две стороны, которые равны. То есть, AABD - ДАВС.

Доказательство ACDE - AABC:
Мы знаем, что CD, это значит, что сторона CD существует.
Мы также знаем, что LB - LD. Это означает, что угол LBD больше, чем угол LDB.
Теперь рассмотрим стороны AC и AB. Мы знаем, что AC - AB. Если AC больше, чем AB, то угол BAC будет меньше, чем угол BCA.
Также мы знаем, что у нас есть равенство CD = CD, это значит, что угол ACD равен углу CDA.
Итак, мы доказали, что у нас есть два угла, которые равны и две стороны, которые равны. То есть, ACDE - AABC.

Надеюсь, эти подробные объяснения помогли вам понять решение данных задач. Если у вас остались еще вопросы, пожалуйста, не стесняйтесь задавать их.