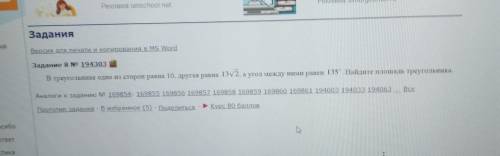
в треугольнике одна из сторон равна 10, другая равна 28, а косинус угла между ними равен 3√11/10. найдите площадь треугольника

Объяснение:

1)

а=10ед

b=28ед

cos<(ab)=3√11/10

S=?

Решение

Тригонометрическое тождество

sin²<(ab)+cos²<(ab)=1

sin<ab=√(1-cos²<(ab))=√(1-(3√11/10)²)=

=√(1-99/100)=√(100/100-99/100)=

=√(1/100)=1/10

S=1/2*a*b*sin<(ab)=1/2*10*28*1/10=14ед²

ответ: 14ед²

2)

а=10ед

b=13√2ед.

<(ab)=135°

sin<(ab)=sin135°=sin45°=√2/2

S=?

Решение

S=1/2*a*b*sin<(ab)=1/2*10*13√2*√2/2=65ед²

ответ: 65ед²

Добрый день! Давай разберем эту задачу пошагово.

У нас есть треугольник, где одна сторона равна 10, другая сторона равна 28 и косинус угла между ними равен 3√11/10. Найдем третью сторону треугольника, используя теорему косинусов.

Теорема косинусов гласит:

c^2 = a^2 + b^2 - 2ab*cos(C),

где c - третья сторона треугольника, a и b - известные стороны, C - угол между ними.

Подставим известные значения в формулу:

c^2 = 10^2 + 28^2 - 2*10*28*cos(C).

Теперь выразим третью сторону треугольника:

c^2 = 100 + 784 - 2*280*cos(C),
c^2 = 884 - 560*cos(C),
c^2 = 884 - 560*(3√11/10).

Так как мы знаем косинус угла (3√11/10), можем подставить его значение:

c^2 = 884 - 560*(3√11/10),
c^2 = 884 - 1680√11/10,
c^2 = (8840 - 1680√11)/10.

Теперь найдем площадь треугольника, используя формулу Герона:

S = √(p*(p-a)*(p-b)*(p-c)),

где S - площадь треугольника, a, b и c - стороны треугольника, p - полупериметр треугольника, который равен сумме сторон, деленной на 2.

Подставим известные значения в формулу:

p = (10 + 28 + c)/2 = (38 + c)/2,
S = √(((38 + c)/2)*(38/2)*(28/2)*(c/2)).

Теперь выразим площадь треугольника, используя третью сторону треугольника:

S = √(((38 + c)/2)*(38/2)*(28/2)*(c/2)),
S = √((c+38)*19*14*c)/4,
S = √(c^2 + 38c) * √266/4.

Так как у нас есть выражение для c^2, можем подставить его значение:

S = √((8840 - 1680√11)/10 + 38*(8840 - 1680√11)/10) * √266/4.

Упростим выражение:

S = √((8840 - 1680√11 + 380 + 38*8840 - 38*1680√11)/10) * √266/4,
S = √(309560/10) * √266/4,
S = √(30956) * √(266)/4,
S = 176 * √(2*7) / 4,
S = 44 * √14.

Итак, площадь треугольника равна 44 * √14.

Я надеюсь, что объяснение было понятным и полезным! Если у тебя появятся еще вопросы, буду рад помочь.