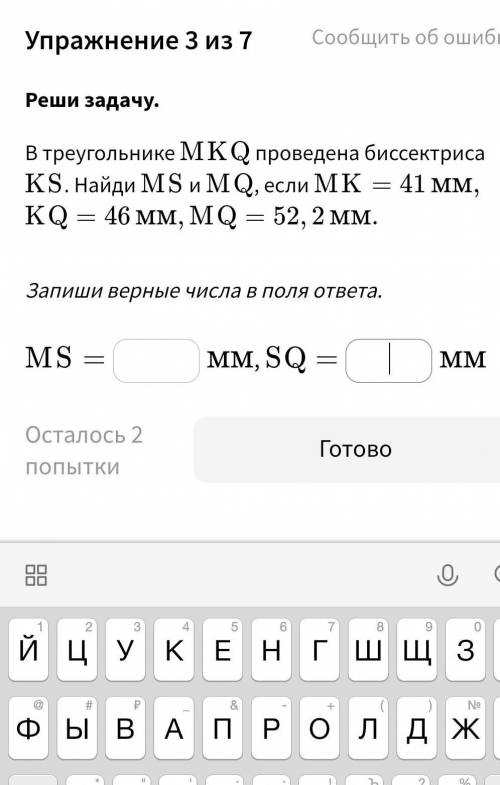
В треуголнике MKQ проведена биссектриса KS. Найди MS и MQ, если MK =41мм, KQ=46мм, MQ=52, 2 мм

Для решения этой задачи, нам необходимо использовать свойства биссектрисы треугольника. Для начала, найдем биссектрису треугольника KS.

1. Найдем длину биссектрисы KS:
Используем теорему биссектрисы, которая утверждает, что биссектриса треугольника делит противоположную сторону пропорционально отношению длин других сторон.
В данном случае, мы знаем, что MK = 41мм и KQ = 46мм.
Поэтому можем записать следующее соотношение:
MK / KQ = MS / SQ
Подставляем известные значения:
41 / 46 = MS / SQ
Теперь, чтобы найти длину MS, нужно найти длину SQ. Для этого воспользуемся фактом, что сумма двух отрезков, создаваемых биссектрисой на основании треугольника, равна длине основания треугольника. В данном случае, это отрезки MS и SQ:
MS + SQ = MQ
Подставляем известные значения:
MS + SQ = 52,2
Теперь у нас есть два уравнения:
41 / 46 = MS / SQ
MS + SQ = 52,2

2. Решим эту систему уравнений. Раскроем первое уравнение и избавимся от дроби:
41 * SQ = 46 * MS
SQ = (46 * MS) / 41

3. Подставим найденное значение SQ во второе уравнение:
MS + (46 * MS) / 41 = 52,2
Упростим уравнение, умножив обе части на 41:
41MS + 46MS = 41 * 52,2
87MS = 2134,2
MS = 2134,2 / 87
MS ≈ 24,51

4. Теперь, когда мы нашли значение MS, можем найти SQ, подставив его в первое уравнение:
SQ = (46 * MS) / 41
SQ = (46 * 24,51) / 41
SQ ≈ 27,49

5. Наконец, чтобы найти MQ, можем воспользоваться вторым уравнением:
MS + SQ = MQ
24,51 + 27,49 = MQ
MQ ≈ 52

Таким образом, мы получили, что MS ≈ 24,51 мм, SQ ≈ 27,49 мм и MQ ≈ 52 мм.