В треугольнике АВС известно, что АС=8, ВС=15, угол С равен 90 градусов. Найдите радиус, описанной около этого треугольника окружности
Другие вопросы по теме Геометрия
Популярные вопросы
- Из одного пункта одновременно в одном направлении выехали два всадника....
1 - Утрьох пробірках без етикеток міститься розчини ферум ii сульфату,...
2 - Писатели 20 века .скажите какие писатели 20 века?...
3 - Преобразуйте в произведение многочлен: 48p^2+72pk+27k^2-27s^2...
1 - Решить уравнения 3 (2y-1)+6(3y-4)=83+5(y-3)...
3 - 1.при разложениибелого светав спектрсильнее . 2.в красного,зеленогои...
2 - Напишите структурные формулы двух алкадиенов,изомерных гекину.назовите...
2 - Какимибудут казатьсязеленые буквына белой бумаге,если смотретьна них...
1 - Придумайте глаголы в неопределённой форме что бы корень у этого глагола...
3 - 3швеи за 6 дней сшили 9 сорочек.сколько дней потребуется одной мастерице...
3
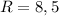 ед.
ед.
Объяснение:Так как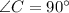 , по условию ⇒
, по условию ⇒ 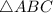 - прямоугольный.
- прямоугольный.
Обозначим центр описанной около треугольника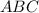 окружности буквой
окружности буквой 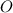 .
.
Центр описанной окружности совпадает с серединой гипотенузы.
Пусть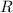 - радиус окружности с центром
- радиус окружности с центром 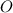 .
.
Найдём гипотенузу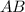 , по теореме Пифагора: (
, по теореме Пифагора: (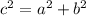 , где
, где  - гипотенуза;
- гипотенуза;  и
и 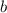 - катеты)
- катеты)
Итак,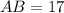 ед. ⇒
ед. ⇒ 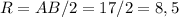 ед.
ед.