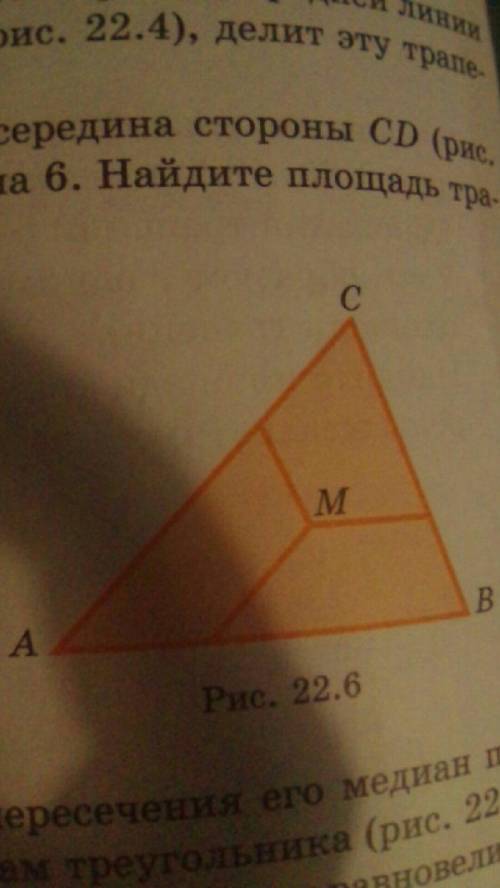
В треугольнике авс через точку м пересечения его медиан проведены отрезки параллельные сторонам треугольника. Докажите что образовавшиеся при этом три трапеции равновелики

Чтобы решить данную задачу, давайте обратимся к основным свойствам треугольников и трапеций.

В данной задаче у нас имеется треугольник АВС и точка М - пересечение его медиан. Также известно, что через точку М проведены отрезки, параллельные сторонам треугольника. Нам нужно доказать, что образовавшиеся при этом три трапеции равновелики.

Для начала, давайте вспомним, что такое медиана треугольника. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данном случае, точка М является пересечением медиан треугольника АВС.

Теперь давайте посмотрим на первую из трех трапеций, которые образуются при проведении отрезков, параллельных сторонам треугольника. Обозначим эту трапецию как МРСН. Здесь М - точка пересечения медиан, Р - середина стороны СВ (укажите на изображении: https://i.imgur.com/PFYk4Hu.png), С - вершина треугольника АВС, а Н - точка на прямой, проведенной через точку С и параллельной стороне АВ.

Обратите внимание, что треугольник СВН равнобедренный, так как из условия задачи сторона ВС параллельна отрезку НР и середина стороны СВ (точка Р) делит сторону СВ на две равные части. Соответственно, углы при основании (стороне СВ) равны.

Важно отметить, что также треугольники МРН и МСН равнобедренные, так как у них соответственно Р и С - середины сторон СВ и ВА, и отрезки РМ и СМ являются медианами треугольника АВС. Из равенства сторон треугольника следует равенство соответствующих углов.

Теперь обратимся ко второй и третьей трапеции, обозначим их как МРВК и МРАВ, соответственно. Мы можем провести аналогичное рассуждение к треугольникам МРВ и МКВ, а также МРА и МКА. Они также будут равнобедренными, так как соответствующие стороны будут равными на основании свойств треугольника (вспомните свойство медиан).

Итак, мы доказали, что все три трапеции - МРСН, МРВК и МРАВ - являются равнобедренными треугольниками. Так как у равнобедренных треугольников равны углы при основании и основания трапеций являются параллельными (со сторонами треугольника), то можно заключить, что все три трапеции равновелики.

Надеюсь, что эта подробная и обстоятельная информация помогла вам понять и доказать заданное утверждение. Если есть еще вопросы, не стесняйтесь задавать.