Геометрия: В треугольнике АВС АС равен 4 корня из 3 АВ=4 ВС =8 Найти уголВ

В треугольнике АВС АС равен 4 корня из 3 АВ=4 ВС =8 Найти уголВ

Ответы

755Никита7451 06.03.2021 12:12

Дано:

AB=4

BC=8

AC=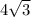 $4\sqrt{3}$

∠B - ?

$cosB = \frac{AB^2 + BC^2 - AC^2}{2*AB*BC} =\frac{4^2+8^2-(4\sqrt{3} )^2}{2*4*8}=0.5\\cosB=0.5\\B=60$

ответ: ∠B = 60°

ПОКАЗАТЬ ОТВЕТЫ

Viktoria818 24.01.2024 10:55

Для решения данной задачи рассмотрим треугольник АВС. В данном треугольнике у нас заранее известные стороны АС, АВ и ВС, а мы хотим найти угол В.

Для начала, найдем сторону ВС. У нас уже есть информация, что ВС = 8.

Затем, найдем сторону АВ. У нас также есть информация, что АВ = 4.

Используя теорему Пифагора, можем найти сторону АС. По теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В нашем случае, это АС. То есть, АС^2 = АВ^2 + ВС^2. Подставляя значения, получим АС^2 = 4^2 + 8^2 = 16 + 64 = 80. Теперь найдем корень из 80, чтобы найти АС. Получаем, что АС = 4√(5).

Зная стороны АС и ВС, мы можем найти угол В, используя косинусную теорему. Косинусная теорема гласит, что квадрат одной из сторон треугольника равен сумме квадратов остальных двух сторон минус удвоенное произведение этих сторон на косинус угла между ними. В нашем случае, ВС^2 = АС^2 + АВ^2 - 2*АС*АВ*cos(В).

Подставляя известные значения, получаем 8^2 = (4√(5))^2 + 4^2 - 2*(4√(5))*4*cos(В). Раскрываем скобки и сокращаем, получаем 64 = 80 + 16 - 8√(5)*cos(В).

Теперь выражаем cos(В), перенося все остальные члены в правую часть уравнения: -80 = - 8√(5)*cos(В).

Далее, делим обе части уравнения на -8√(5), чтобы найти значение cos(В): cos(В) = -80 / (-8√(5)) = 10 / √(5) = 2√(5).

Наконец, можем найти угол В, используя обратную функцию косинуса (арккосинус): В = arccos(2√(5)).

Ответ: Угол В равен arccos(2√(5)).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия