В треугольнике ABC угол C прямой, угол А = 60°, AB = 28 см. Проведена окружность с центром в точке A. Каким должен быть её радиус, чтобы она касалась прямой BC. ответ дайте в сантиметрах.
варианты ответов: 12см, 13см, 15см, 14см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Устное сообщение об эпизоде борьбы русского народа...
1 - Составьте составьте предложение со слов Я благодарна вам или Я благодарна...
2 - А м. Муратова, К. ж. АртыковМУЗЫКАе...
2 - Составить маршрут космического путешествие...
3 - Бедные греки почти не употребляли в пищучто? скажите ...
2 - ответы на вопрос по гуннам...
2 - Написать расказ про Моде По Истории Казахстана ...
3 - Метоморфты деген не және қандай тау жыныстары жатады?жаратылыс тану...
1 - Проект по английскому языку (ты есть то что ты ешь ) 15 предложений...
3 - Роль краеведения в образовании школьников эссе ...
1
14 см
Объяснение:
По свойству касательной к окружности она должная быть перпендикулярна радиусу. В данном случае т.к. AС ⊥ BC (по условию ∠С =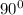 ) и центр окружности в точке А, то АС и есть тот радиус, который нужно найти.
) и центр окружности в точке А, то АС и есть тот радиус, который нужно найти.
Но АС лежит напротив угла B, а ∠B =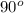 - ∠A =
- ∠A = 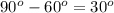 , таким образом ∠B =
, таким образом ∠B = 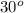
Известно, что катет, лежащий напротив угла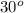 равен половине гипотенузы/
равен половине гипотенузы/
AB - гипотенуза и по условию AB = 28, ⇒ AC = 28 : 2 = 14 (см)