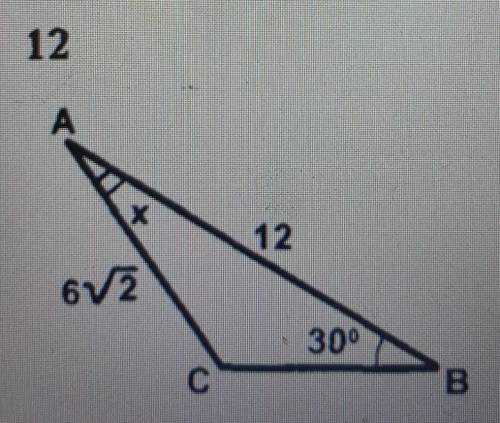
В треугольнике abc большая сторона AB=12 см ac= 6 корней из 2, угол B=30, УГОЛ A=X Найдите

Объяснение:

am am I to cook with glass but I was discussing you

Для решения этой задачи нам понадобятся знания о треугольниках и тригонометрии.

Дано: треугольник ABC, где AB = 12 см, AC = 6√2 см и угол B = 30 градусов. Нам нужно найти угол A (обозначен как X на рисунке).

Для начала, давайте предположим, что угол A равен Y градусов. Тогда у нас будет две известные стороны и один известный угол в треугольнике, что позволяет нам использовать тригонометрию.

Обратимся к соотношению синуса в треугольнике:

sinY = противолежащая сторона / гипотенуза.

В нашем случае, гипотенуза - это сторона AB, а противолежащая сторона - это сторона AC. Исходя из данных, у нас есть соотношение:

sinY = AC / AB.

Подставляем значения:

sinY = (6√2 см) / (12 см).

Делаем упрощение в числителе дроби:

sinY = (6 см * √2) / (12 см).

Делим и числитель, и знаменатель на 6:

sinY = (√2 см) / (2 см).

Теперь нам нужно найти arcsin (обратный синус) от этого значения, чтобы найти угол Y.

Поскольку sinY = (√2 см) / (2 см), используем калькулятор и находим:

Y ≈ 45 градусов.

Теперь нам нужно найти угол X, который задается вопросом.

Углы треугольника в сумме равны 180 градусов. Таким образом:

X + Y + угол C = 180 градусов.

Подставляем известные значения:

X + 45 градусов + 30 градусов = 180 градусов.

Складываем два известных угла и вычитаем из 180 градусов:

X + 75 градусов = 180 градусов.

Вычитаем 75 градусов из обеих сторон уравнения:

X = 180 градусов - 75 градусов.

X = 105 градусов.

Таким образом, получаем ответ: угол A равен 105 градусов.