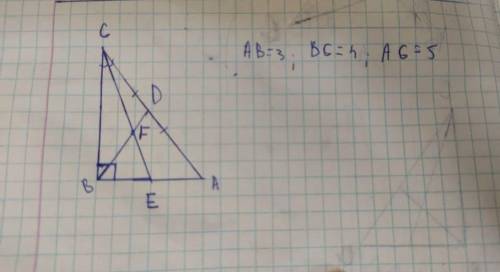
В треугольнике ABC AB= 3 BC=4 ; AC=5 ; если СE биссектриса угла ACB ; a BD является медианной AC . И СE пересекается c BD в точке F
То найдите
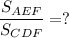
Другие вопросы по теме Геометрия
Популярные вопросы
- Вырежи из бумаги квадрат с длиной стороны 6 см. докажи перегибанием что каждая...
3 - 4әріп, 5 дыбыстан тұратын сөз,2 әріп, 3 дыбыстан тұратын сөз,5 әріп ,4 дыбыстан...
3 - Найди длину стороны треугольника у которого все стороны равны и периметр...
3 - Написать о каком нибудь персонаже, на !...
1 - Решите 4cos(25п/12)+4sin(19п/12)/-4cos(п/12)-2cos(11п/12)...
3 - Перевести: controlled me. my mind and body. even now, after his death. that...
2 - Каким было хозяйство у зависимого крестьянина...
1 - Внекоторый момент времени аня измерила угол между часовой и минутной стрелками...
2 - На мутном небе мгла носилась орфограммы в предложении...
3 - Найдите мне сказку шапка полная небылиц ! не как не могу найти : (. ещё раз...
1
т о биссектрисе
BE/EA =BC/CA =4/5
т Менелая
AD/DC *CF/FE *EB/BA =1 => 1/1 *CF/FE *4/9 =1 => CF/FE =9/4
Площади треугольников с равными высотами относятся как основания.
S(AEF)=x, S(CDF)=S(ADF) =y
S(AFC)/S(AEF) =CF/FE =9/4 =2y/x => S(AEF)/S(CDF) =x/y =8/9
Другое решение
BF/FD =BC/CD =4 :5/2 =8/5 (т о биссектрисе)
S(BCF)/S(CDF) =BF/FD =8/5 => S(CDF)=5/8 S(BCF)
S(ABD)=S(CBD), S(AFD)=S(CFD) => S(BCF)=S(BAF)
BE/EA =BC/CA =4/5 (т о биссектрисе)
S(BFE)/S(AEF) =BE/EA =4/5 => S(AEF) =5/9 S(BAF)
S(AEF)/S(CDF) =5/9 :5/8 =8/9