В треугольник АВС AB = BC. Луч СK - биссектриса угла ВСМ. Найдите градусную меру угла A, если угол BCK = 70°.
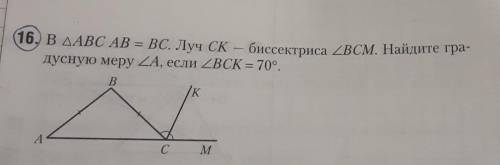
Другие вопросы по теме Геометрия
Популярные вопросы
- Мнимое изображение предмета находится на расстоянии 0,8 м от...
2 - Мнимое изображение предмета находится на расстоянии 1,3 м от...
2 - На каком расстоянии от двояковыпуклой линзы с фокусным расстоянием...
2 - На каком расстоянии от двояковыпуклой линзы с оптической силой...
3 - Предмет расположен на расстоянии 40 см от линзы с оптической...
2 - Расстояние от изображения до рассеивающей линзы составляет 0,75...
2 - Главное фокусное расстояние рассеивающей линзы равно 18 см....
1 - На каком расстоянии от собирающей линзы с фокусным расстоянием...
1 - Действительное изображение предмета, полученное с собирающей...
2 - Определите увеличение, даваемое линзой, фокусное расстояние...
1
Мы можем представить треугольник ABC таким образом:
A
/ \
/ \
B-----C
Дано, что AB = BC. Это означает, что углы ABC и BCA равны между собой, потому что треугольник равнобедренный.
Далее, луч CK - биссектриса угла ВСМ, что означает, что угол BCK делит угол BCM на два равных угла. Таким образом, угол BCA = 2*угол BCK.
Из условия известно, что угол BCK равен 70°.
Теперь мы можем найти угол BCA:
угол BCA = 2*угол BCK = 2*70° = 140°.
Так как треугольник равнобедренный, углы ABC и BCA равны. Следовательно, угол ABC = угол BCA = 140°.
Но мы искали угол A. Поскольку сумма углов треугольника равна 180° (сумма углов в треугольнике), то угол A равен:
угол A = 180° - угол BCA - угол ABC = 180° - 140° - 140° = 180° - 280° = -100°.
Обычно в задачах градусная мера угла не может быть отрицательной. Поэтому в данном случае треугольника с такими условиями не существует.