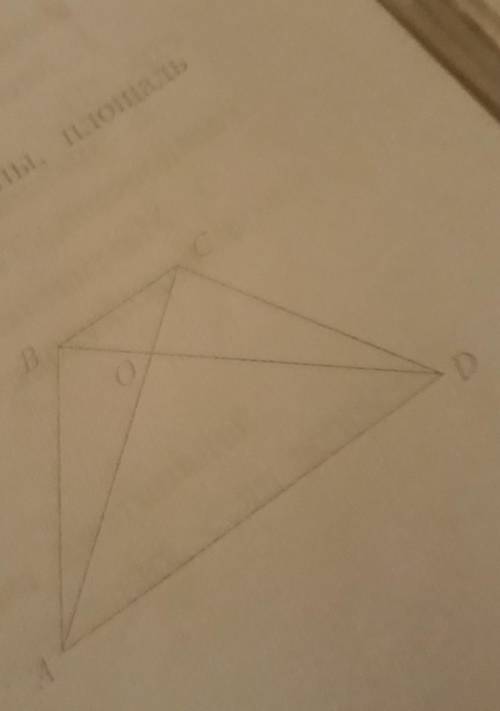
В трапеции АВСD диагонали АС и ВД пересекаются в точке О. S- площадь ВОС=4см^2
S-площадь АОD=16см^2
а) Найдите площадь треугольника АОВ
б) Найдите площадь трапеции АВСD
в конце книги ответ
а) 8см^2
б) 36см^2
начертите чертёж напишите дано и решение
можно чуть-чуть быстрей
Другие вопросы по теме Геометрия
Популярные вопросы
- Решить две бригады работая вместе висадили деревья за 12 дней.сколька...
3 - Решите,, 1)найти количество вещества,которое содержится в 5,6 литров...
3 - 30 ) grammar practice complete these sentences with the correct form...
3 - 20 примеров тел и веществ, например: мяч-...
1 - Лабораторная работа по теме: влияние факторов окружающей среды местной...
3 - Бежит, долине, береговыми-морфологически разбор...
2 - Значение римских цифр и правила построения...
1 - Маленькое, дано: а больше 2 и б меньше 3.поставьте вместо многоточия...
1 - Опредильть сколько лет просушествовала римская империя если рим 753 году...
2 - Какие стили речи в книжном направлении...
3
.............
Объяснение:
Дано: Трапеция АВСД.
Диагонали АС и ВД.
S(BOC)=4см^2
S(AOD)=16см^2
Найти: S(AOB) и S(ABCD)-?
Решение во вложении.
Объяснение:
1) Т.к. треугольники, образованные основаниями и отрезками диагоналей подобны, то ΔВОС~ΔАОD и :
ВО : ОD= ОС : ОА = ВС : АD, а так же как h₁ : h₂, где h₁ и h₂ - высоты соответствующих треугольников.
Кроме того,
SΔвос : SΔaod = ВС² : АD² → 4 : 16 = ВС² : АD², откуда
ВС = √4 =2см
АD = √16 = 4см
2) h₁ : h₂ = ВС : АD = 2/4 = 1/2
SΔвос = ½ ВС*h₁ = 4(см²), тогда
h₁ = 4*2/2 = 4(см)
SΔaod = ½АD*h₂ = 16(см²) , откуда
h₂ = 16*2/4 = 8(см)
h = h₁ + h₂ = 4 + 8 = 12(см)
3) Sавcd = (DC + AВ) * h /2 =(2+4)*12/2 = 36(см²) = площадь трапеции
4) Треугольники, образованные отрезками диагоналей и боковыми сторонами, равновелики, т.е.
SΔаов = SΔсоd = (Sавcd - SΔвос - SΔaod) / 2 =
= (36 - 4 - 16)/2 = 16/2 = 8 (см²)