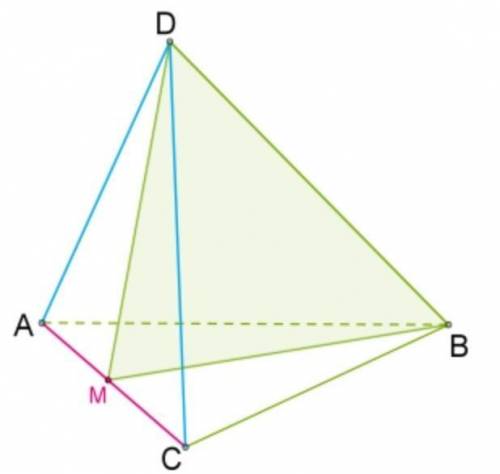
В тетраэдре DABC точка M отмечена на середине ребра AC. Известно, что в этом тетраэдре
BA=BC;DA=DC.
Докажи, что прямая, на которой находится ребро AC, перпендикулярна плоскости (BDM).
1. Определи вид треугольников АВС и DAC
2. Какой угол образует медиана с основанием этих треугольников?
ответ: ... градусов.
3. Согласно признаку, если прямая ... к ... ... прямым в некой плоскости, то она ... к этой плоскости.
Другие вопросы по теме Геометрия
Популярные вопросы
- Какие измения произошли в науке при петре 1...
2 - Назвать главных героев н. в. гоголя ( тарас бульба ) по 1 главе?...
1 - Самой элементарной формой организации является : а) натуральное хозяйство...
1 - Уравнение а)4/15: x=2/5 б) у- 7/12у = 4 1/6...
1 - Побудувати ланцюг живлення що склався на болоті: чапля-жаба-комаха-рослина?...
3 - Водном из ниже предложений неверно употреблено выделенное слово.исправьте...
1 - Сколько сотен содержится в тридцати миллионах...
1 - Иван 10 секунд записывал двухканальную стерео запись с частотой дискретизации...
1 - Где нужно поставить запятую в предложении ? поэзия воспевает то величавые...
3 - Кто нибудь знает,кто виноват в том что любовь не состоялась в романе отцы...
2
1. Определим вид треугольников АВС и DAC:
Из условия BA=BC и DA=DC следует, что треугольники АВС и DAC являются равнобедренными.
В треугольнике АВС сторона BA равна стороне BC, следовательно, угол ВАС равен углу ВСА. Аналогично, в треугольнике DAC угол DАС равен углу DАС.
2. Определим, какой угол образует медиана с основанием треугольников АВС и DAC:
Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
В нашем случае, медиана треугольника АВС - это отрезок BM, а медиана треугольника DAC - это отрезок DM.
Так как точка М является серединой ребра АС, то отрезок BM и отрезок DM равны между собой и равны половине длины ребра АС.
3. Рассмотрим плоскость BDM и докажем, что прямая, на которой находится ребро AC, перпендикулярна этой плоскости:
Пусть прямая, на которой лежит ребро АС, пересекает плоскость (BDM) в точке K.
Требуется доказать, что прямая АС перпендикулярна плоскости (BDM), то есть угол AKD равен 90 градусов.
Докажем это от противного. Предположим, что угол AKD не равен 90 градусов, то есть прямая АС и плоскость BDM не перпендикулярны.
Возьмем плоскость (BDM), параллельную плоскости (BDM) и проходящую через прямую АС, и обозначим ее XZY.
Очевидно, что треугольник AKD и треугольник XZK подобны, так как у них соответственные углы равны.
Так как в треугольниках АВС и DAC углы ВАС и DАС равны, то и углы DKC и BKC равны, так как треугольники DKC и BKC также являются равнобедренными.
Возьмем медианы треугольников AKD и XZK. По свойству медиан, они делятся в отношении 1:2 (то есть каждая медиана делит противоположную сторону на две равные части).
Пусть точка L - точка пересечения медиан треугольников AKD и XZK.
Так как медианы треугольников AKD и XZK пересекаются в точке L, которая делит каждую из них в отношении 1:2, то точка L является серединой линии, соединяющей точки К и М.
То есть Л должна совпадать с М, так как по условию М - середина ребра АС.
Таким образом, мы приходим к противоречию: точка L должна равняться М, но, предполагая, что угол AKD не равен 90 градусов, мы пришли к выводу, что Л равняется М.
Следовательно, наше предположение неверно, и угол AKD равен 90 градусов.
Таким образом, мы доказали, что прямая, на которой находится ребро АС, перпендикулярна плоскости (BDM).