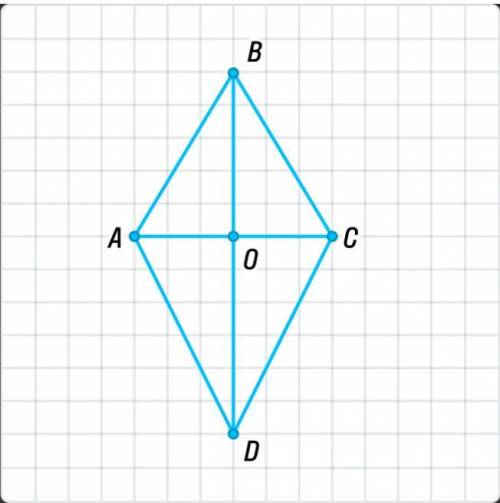
В ромбе ABCD сторона AB=15,диагональ BD=24.Найди диагональ AC.

Другие вопросы по теме Геометрия
Популярные вопросы
- как умножать дроби на корни?? решить: 1/2 умножить на √121 - √0,16...
1 - В двух бочках вместе 580 л бензина. Когда из первой бочки взяли 23 бензина,...
1 - x=10+5 x=15 Не знаю правельно или нет я сама думаю......
2 - помагите вопросы:в самалтёте была 1000 керпичов один упал сколько кирпич...
2 - 1. Have you got a hobby? If yes, what is it? 2. How long have you had...
3 - Серёжа загадал известного(ную) спортсмена(нку), а Паше нужно его(её)...
2 - 1. Провести анализ отдельных газовых участков процессов (участки 1-2,2-3,...
2 - Изменения геополитического положения РФ с связи с расширением Евросоюза...
1 - Составьте диаграмму Венна,сравните произведение Шекспира Ромео и Джульетта...
1 - Дайте описание картины зимнее кружево В. К. Бруля...
3
18.
Объяснение:
Дано: ABCD - ромб.
АВ = 15; BD = 24.
Найти: АС
1. Рассмотрим ромб ABCD. Так как ромб, то все его стороны равны между собой. Поэтому AB = BC = CD = AD = 15. Отметим это на рисунке.
2. Мы также знаем, что диагональ BD равна 24. Отметим ее на рисунке.
3. Раз ромб ABCD - это параллелограмм, то применяем свойства параллелограмма. Одно из таких свойств состоит в том, что диагонали параллелограмма делятся пополам. Поэтому BD = 2 * AC.
4. Используя это свойство, мы можем найти длину диагонали AC. Для этого делаем следующее:
AC = BD / 2 = 24 / 2 = 12.
Ответ: Длина диагонали AC составляет 12.