1. Геометрия
  2. В ромбе ABCD AC больше BD и АС/BD

В ромбе ABCD
AC больше BD и АС/BD - BD/AC = 2√3
Найдите угол A

ВиГуки247 ВиГуки247    2   07.08.2022 06:57    1

Ответы
Georgeo19rus Georgeo19rus  07.08.2022 06:58

\frac{\pi }{6}

Объяснение:

Информация, что диагональ ромба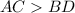 AC BD говорит о том, что \angle A — острый.

Пусть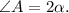 \angle A = 2\alpha . Так как диагонали ромба являются биссектрисами его углов,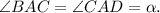 \angle BAC = \angle CAD = \alpha .

Из метрических соотношений в прямоугольном треугольнике

{\mathop{\rm ctg}\nolimits} \alpha = \displaystyle\frac{{AO}}{{BO}} = \displaystyle\frac{{2AO}}{{2BO}} = \displaystyle\frac{{AC}}{{BD}},

и наоборот,

\displaystyle\frac{1}{{{\mathop{\rm ctg}\nolimits} \alpha }} = {\mathop{\rm tg}\nolimits} \alpha = \displaystyle\frac{{BD}}{{AC}}.

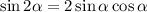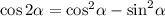Тогда по условию, а затем с применением формул синуса и косинуса двойного угла \sin 2\alpha = 2\sin \alpha \cos \alpha  и \cos 2\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha:

{\mathop{\rm ctg}\nolimits} \alpha - {\mathop{\rm tg}\nolimits} \alpha = 2\sqrt 3 ;\\

\displaystyle\frac{{\cos \alpha }}{{\sin \alpha }} - \displaystyle\frac{{\sin \alpha }}{{\cos \alpha }} = 2\sqrt 3 ;\\

\displaystyle\frac\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\sin \alpha \cos \alpha }} = 2\sqrt 3 ;\\

\displaystyle\frac{{\cos 2\alpha }}{{\sin 2\alpha }} = \sqrt 3 ;\\

{\mathop{\rm ctg}\nolimits} 2\alpha = \sqrt 3 ;\\

2\alpha = \displaystyle\frac{\pi }{6}.


В ромбе ABCD AC больше BD и АС/BD - BD/AC = 2√3 Найдите угол A
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
redle01 redle01  12.05.2019 12:02
Вравнобедренном треугольнике авс ас основание. проведена высота вн. сторона ав =29см, вн=21см. найдите площадь треугольника авс​...
nasyi nasyi  12.05.2019 11:57
На рисунке углы c и e равны 90 0 найти a e если известно, что a d = 35 , e c = 20 , d b = 35 ....
BatsonPlay BatsonPlay  12.05.2019 11:56
Стрелочка написать слова нос​...
nikita200310266xcute nikita200310266xcute  08.05.2020 15:14
Центрі P нүктесі болатын шеңбердің AB диаметріне KN хордасы перпендикуляр жүргізілген. Шеңбердің радиусы 14см, ал бұрыш KPA=30° екені белгілі болса, KNP үшбұрышының периметрін...
megachiglakov megachiglakov  08.05.2020 15:14
Прямокутний трикутник abc,ab=5см,кут c=кут у.Знайдіть bc...
Yaroslava1902 Yaroslava1902  08.05.2020 15:14
Верны ли утверждения:1) В прямоугольном треугольнике медиана, проведённая из вершины прямого угла в два раза больше гипотенузы.2)Верно ли, что прямоугольный треугольник равны...
ALexus67 ALexus67  08.05.2020 15:13
До ть будь ласка дуже требаа​...
yunis2007 yunis2007  08.05.2020 15:13
На рисунке изображены треугольники MKT и KTN. ∠MKN = 50°. Найдите числовое значение ∠MKT. За полное решение...
НектоПожизни НектоПожизни  06.10.2019 12:10
Найдите площадь треугольника, две стороны которого равны 3см и 8см, а угол между ними равен а) 30° б) 45° в) 60° г) 90°....
Klimg Klimg  06.10.2019 11:04
Окружность задана уравнением (х+1)? + (у – 2)2 = 9. напишите уравнения прямых, проходящих через её центр и параллельных оси абсцисс и оси ординат....

Популярные вопросы