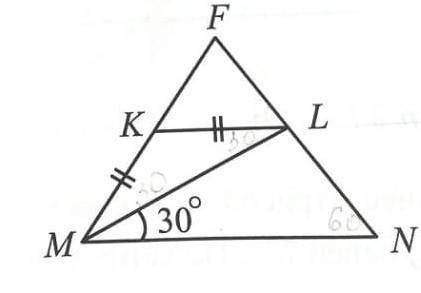
В равностороннем треугольнике MFN с основанием MN и углом N. раз ным 60°, проведён отрезок KL так, что угол LMN равен 30°, MK = KL Докажите, что KL || MN. Найдите угол КLF. Запишите решение и ответ. ​

Доказательство:

Для начала, давайте обратим внимание на то, что треугольник MFN является равносторонним треугольником с углом N, равным 60°.

Теперь рассмотрим отрезок KL. У нас есть информация о том, что угол LMN равен 30°, а MK равна KL.

Нам нужно доказать, что KL || MN и найти угол КLF.

Для доказательства параллельности отрезков KL и MN мы можем использовать угловую аксиому. Если две прямые пересекаются третьей, и сумма смежных углов равна 180°, то эти две прямые параллельны друг другу.

Первый шаг: Найдем угол М.

Угол М равен 180° минус (угол МКL, равный 30°) минус (угол LMK, который мы ищем).

Угол М = 180° - 30° - LMK.

Так как треугольник MFN является равносторонним, то угол М равен 60°.

60° = 180° - 30° - LMK.

Упростив это уравнение, мы получаем:

LMK = 180° - 30° - 60°.

LMK = 90°.

Теперь у нас есть информация о значении угла LMK, который равен 90°.

Второй шаг: Докажем параллельность отрезков KL и MN.

Для этого мы воспользуемся угловой аксиомой.

У нас есть два угла: угол LMK (90°) и угол N (60°).

Сумма этих углов должна быть равна 180°.

LMK + N = 90° + 60° = 150°.

Если KL и MN пересекаются, то сумма смежных углов должна быть равна 180°.

Так как сумма углов LMK и N не равна 180°, это означает, что отрезки KL и MN не пересекаются, и следовательно, они параллельны.

Третий шаг: Найдем угол КLF.

У нас есть две параллельные прямые: KL и MN.

Когда прямые параллельны, то соответствующие углы равны.

Угол КLF равен углу LMK.

Теперь мы знаем, что угол КLF равен 90°.

Решаемая проблема состоит в том, чтобы доказать, что KL || MN и найти угол КLF.

Решение:
1. Угол КLF равен 90°.
2. KL и MN параллельны.

Ответ:
KL и MN параллельны, и угол КLF равен 90°.