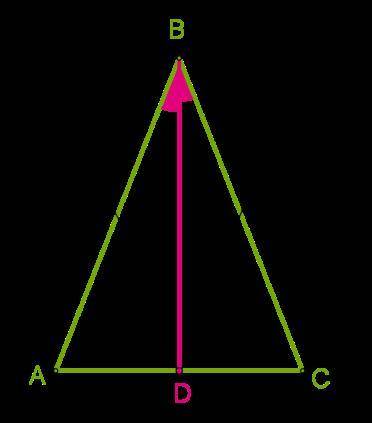
В равнобедренном треугольнике с длиной основания 77 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.
Другие вопросы по теме Геометрия
Популярные вопросы
- 1. Сколько литров кислорода выделится при разложении 10 моль воды?...
1 - Найти предложения, в которых запятая между частями сложносочиненного...
1 - Как на примере оброзов Гринева и Швабрина из повести Капитанская дочка...
3 - Активное сопротивление R и индуктивность L соединены параллельно и...
2 - Match sentences 1-5 with reasons a-e using because...
3 - Информатика. Укажите верно записанную формулу: = ЕСЛИ (А3 = 5; В4*...
1 - Скільки срібла виділяється при оксигенні 22 г. оцтового альдегіду...
1 - Решите буду песат бред 20 букв надо ...
3 - Дайте характеристику кислорода как простому веществу.ХЕЕЕЛП ...
3 - Task II. Writing. Write an essay on the theme “It is better to live...
1
У нас есть равнобедренный треугольник ABC, в котором основание BC имеет длину 77 см. Проведена биссектриса угла ABC, которую мы обозначим как BD.
Чтобы доказать, что отрезок BD является медианой, мы должны убедиться, что он делит сторону AC пополам. Для доказательства мы воспользуемся вторым признаком равенства треугольников, который гласит: если два угла и одна сторона одного треугольника равны соответственно двум углам и одной стороне другого треугольника, то эти треугольники равны.
В нашем случае, треугольник ABC является равнобедренным, поэтому угол ABC равен углу ACB. Мы также знаем, что угол ABD равен углу CBD, так как BD - биссектриса угла ABC. Следовательно, у нас есть два равных угла.
Теперь давайте рассмотрим отрезок AD. Мы хотим определить его длину.
Мы знаем, что отрезок BD является биссектрисой угла ABC. Это означает, что угол ABD равен половине угла ABC. А так как треугольник ABC равнобедренный, угол ABC равен углу ACB. Таким образом, угол ABD равен половине угла ACB.
Теперь у нас есть два треугольника: треугольник ABD и треугольник CDB. У них вершина D общая и у них равны два угла ABD и CBD. Мы также знаем, что сторона BD равна самой себе. Исходя из второго признака равенства треугольников, мы можем заключить, что эти два треугольника равны.
Далее, поскольку эти треугольники равны, то сторона AD будет равна стороне CD. То есть, отрезок AD делит сторону AC пополам.
Теперь мы можем найти длину отрезка AD.
Мы знаем, что сторона BC (или AC) равна 77 см. Так как отрезок AD делит сторону AC пополам, то длина отрезка AD будет 77 см / 2, что равно 38.5 cм.
Таким образом, мы доказали, что отрезок BD является медианой и определили длину отрезка AD, которая составляет 38.5 см.