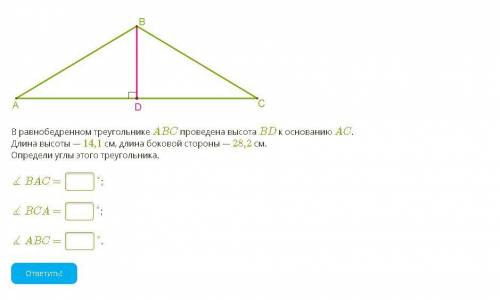
В равнобедренном треугольнике ABC проведена высота BD к основанию AC. Длина высоты — 14,1 см, длина боковой стороны — 28,2 см.
Определи углы этого треугольника.
∡ BAC =
°;
∡ BCA =
°;
∡ ABC =
°.
Другие вопросы по теме Геометрия
Популярные вопросы
- у царя Гвидона 3 сына.У каждого сына по 3 сына,а у каждого внука...
2 - Разберите предложения Ель обычно растёт на влажных местах и Очень...
2 - 15. Начните составлять таблицу Развитие украинской культуры в XVI...
3 - Исполняя свои обязанности, сторож Петров получил пулевое ранение...
3 - АВСД А1 В1 С1 Д1 - куб. Вказати точку перетину прямої АС та площини...
2 - Определить величины реакций для балки с шарнирными опорами. Провести...
2 - Put in the right preposition: at, back, for, on/upon, out. Translate...
1 - 1.Из предложенного перечня выпишите отдельно названия тела и вещества:...
3 - Размножение кишечнополостных животных?...
1 - Какие интонации преобладают в чтении народной артисткой России...
3
∡ BAC = 30°; ∡ BCA = 30°; ∡ ABC = 120°.
Объяснение:
1) В прямоугольном треугольнике ABD боковая сторона АВ = 28,2 см является гипотенузой, а высота BD = 14,1 см - катетом.
Так как данный катет в 2 раза меньше гипотенузы, то это означает, что угол ВАС, против которого лежит катет ВD, равен 30°.
∡ BAC = 30°
2) В равнобедренном треугольнике углы при основании равны, поэтому:
∡ BCA = ∡ BAC = 30°
3) Угол АВС равен разности между суммой внутренних углов треугольника (180°) и углами при основании:
∡ ABC = 180 - ∡ BCA - ∡ BAC = 180 - 30 - 30 = 120°.
ответ: ∡ BAC = 30°; ∡ BCA = 30°; ∡ ABC = 120°.