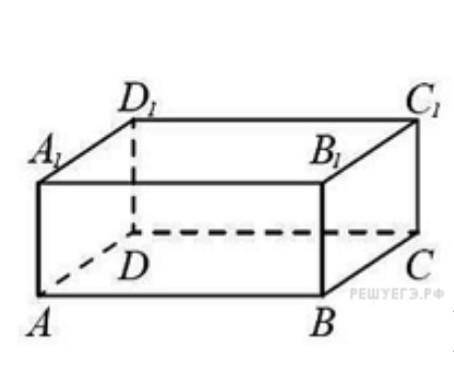
В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра CD, CB и диагональ CD1 равны соответственно 5, 6 и √29 . Найдите объём параллелепипеда ABCDA1B1C1D1.
Другие вопросы по теме Геометрия
Популярные вопросы
- Ссхемы горнера разделиие многочлен а(х) на многочлен в(х),укажите...
2 - Вырази в мл: 1,2 л; 0,50 л; 0.040 л; 0,006 л....
2 - Таблица по типу круглых червей название червях, где обитает...
1 - Вырази в литрах: 1,2 мл; 28 мл; 435 мл; 1823 мл....
2 - Фанетычны разбор слоў 1) інтэр е 2) сям я сінтаксічны разбор...
1 - Сколько процентов составляет смешанная дробь 12,25 от числа...
1 - Сравнить сказание о потопе из библии и миф о потопе шумеров....
3 - Составить схему совместимости групп крови при переливании, объяснить...
1 - Составить схему этапов свертывания крови....
1 - Как вы думвете почему узник стало популярной народной песней?...
3
ответ: V=60
Объяснение: если записать значения сторон в том порядке в котором они даны, а именно: СД=5; СВ=6; СД1=√29, то для начала найдём ДД1 по теореме Пифагора: ДД1²=СД1²-СД²
ДД1²=√29²-5²=29-25=4; ДД1=√4=2
ДД1=2. Теперь найдём объём параллелепипеда, зная его длину, ширину и высоту по формуле:
V=СД×СВ×ДД1=5×6×2=60