1. Геометрия
  2. В прямоугольнике ABCD

В прямоугольнике ABCD AB = 12, ВС = 8, М – середина стороны АВ. Найдите длины векторов |DC→| , |MC→|, |MA→| Выберите один ответ:

a. |DC→| =12 , |MC→| = 11, |MA→|=6

b. |DC→| =10 , |MC→| = 10, |MA→|=5

c. |DC→| =11 , |MC→| = 10, |MA→|=8

d. |DC→| =12 , |MC→| = 10, |MA→|=6

микс111111 микс111111    2   05.08.2021 14:02    64

Ответы
Анюта10072401 Анюта10072401  04.09.2021 16:19

d.  |DC→| =12 , |MC→| = 10, |MA→|=6

Объяснение:

DC и АВ - противоположные стороны прямоугольника, поэтому

|\overline {DC}| =|\overline {AB}| = 12

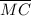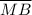Векторы \overline {MC}, \overline {MB}, \overline {BC} образуют прямоугольный треугольник МВС с гипотенузой МС

\overline {MC} = \overline {MB}+ \overline {BC}

|\overline {MB}| =0.5|\overline {AB}| = 6

|\overline {MC}| = \sqrt{|\overline {MB}|^2+|\overline {BC}|^2}} = \sqrt{6^2 + 8^2} = 10

Вектор \overline {MA}=-0.5\overline {AB}, поэтому

|\overline {MA}| =0.5|\overline {AB}| = 6

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
daniel9876 daniel9876  30.05.2019 23:40
Втреугольнике abc стороны ac и bc равны, ab = 12, cos a =2√5/5. найдите высоту ch...
linagurova6545 linagurova6545  04.06.2019 12:00
Втреугольнике abc стороны ab=8см, bc=15см, ac=17см. найдите угол, противолежащий большей стороне треугольника. решите надо...
Sashok1252535 Sashok1252535  04.06.2019 12:00
Центральный угол aob опирается на хорду ав так, что угол оав равен 60°. найдите длину хорды ав, если радиус окружности равен 8....
NOKANplay NOKANplay  04.06.2019 12:00
Боковые стороны трапеции, описанной около окружности, равны 23 и 3. найдите среднюю линию трапеции...
Юлия757445 Юлия757445  04.06.2019 12:00
Высота правильной четырёх правильной пирамиды равна h .а боковое ребро составляет с основанием угол α.найдите площадь полной поверхности пирамиды...
vladborhovp0a44d vladborhovp0a44d  04.06.2019 12:00
Центральный угол на 27o больше острого вписанного угла, опирающегося на ту же дугу окружности. найдите вписанный угол. ответ дайте в градусах....
Shizuka494 Shizuka494  04.06.2019 12:00
Впрямоугольном треугольнике авс гипатинуза равна 10 см, а один катетов равен 6 см.найти другой катет?...
abduabdu2015 abduabdu2015  04.06.2019 12:00
Найдите площадь круга, длина окружности которого составляет 20 умноженное на корень из пи....
Kek1928 Kek1928  04.06.2019 12:00
Втреугольнике авс ав = 5 корней из 2, угол а = 30 градусов,угол с= 45 градусов. найдите вс...
ketti336 ketti336  04.06.2019 12:00
Угол между стороной правильного n угольника вписанного в окружность и радиусом этой этой окружности проведенным в одну из вершин стороны равен 75 градусам найдите n...

Популярные вопросы