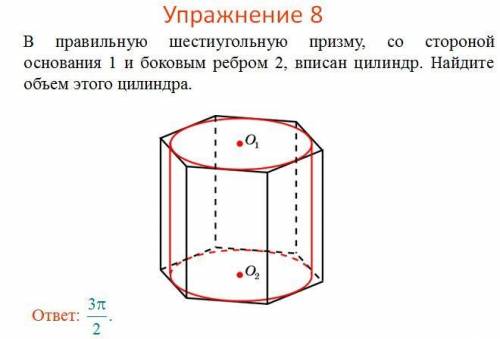
В правильную шестиугольную призму, со стороной основания 1 и боковым ребром 2, вписан цилиндр. Найдите объем этого цилиндра.

Для решения данной задачи, давайте разобьем ее на несколько подзадач. Во-первых, нам нужно найти радиус окружности, описанной вокруг основания цилиндра. Для этого мы можем воспользоваться свойством правильных шестиугольников.

Как известно, в правильном шестиугольнике все стороны и углы равны между собой. Рассмотрим треугольник, образованный двумя радиусами окружности и одним из сторон правильного шестиугольника.

Мы знаем, что сторона основания призмы равна 1. Радиус окружности можно найти, разделив сторону на 2√3. Следовательно, радиус окружности равен 1 / (2√3).

Далее, нам нужно найти высоту цилиндра. Обратите внимание, что высота цилиндра равна боковому ребру призмы, то есть 2.

Известно, что объем цилиндра можно найти по формуле V = πr²h, где V - объем, r - радиус основания, h - высота.

Подставим полученные значения в формулу и рассчитаем объем:
V = π * (1 / (2√3))² * 2.

Давайте посчитаем это выражение:

V = π * (1 / (4 * 3)) * 2
V = π * (1 / 12) * 2
V = π / 6

Ответ: объем этого цилиндра равен π / 6.

Таким образом, объем цилиндра, вписанного в данную призму, равен π / 6."