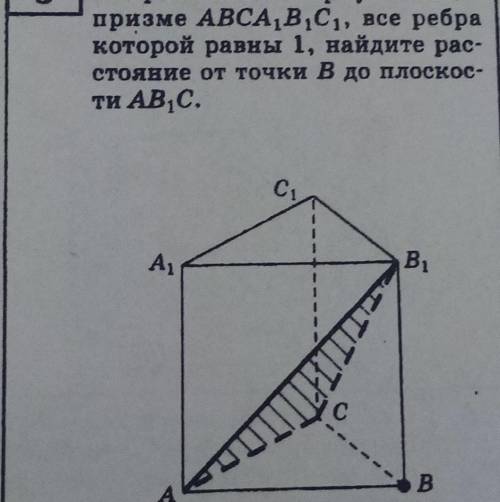
В правильной треугольной призме ABCA1B1C1 все ребра которой равны 1,найдите расстояние от точки B до плоскости )

Для того чтобы найти расстояние от точки B до плоскости, нам понадобятся некоторые знания о геометрии и применение формулы.

Перед тем, как приступить к решению, определим некоторые обозначения. Пусть точка D - проекция точки B на плоскость ABCA1B1C1, а точка P - центр основания треугольной призмы ABCA1B1C1.

Нам известно, что треугольная призма ABCA1B1C1 правильная, поэтому все углы равны 60 градусов. Также известно, что все ребра призмы равны 1.

Сначала построим высоту треугольника ABC. Она будет проходить через вершину А и перпендикулярна плоскости ABCA1B1C1. Поскольку треугольник ABC является равносторонним, высота будет разделять его на два равнобедренных треугольника.

Теперь найдем длину высоты треугольника ABC. Поскольку треугольник ABC равносторонний со сторонами 1, то также известно, что его высота делит его на два равнобедренных треугольника со сторонами 1, 1 и h, где h - высота. По теореме Пифагора, для такого треугольника высота будет равна h = √(1^2 - 0.5^2) = √(1 - 0.25) = √0.75 = 0.866.

Теперь у нас есть все необходимые данные для нахождения расстояния от точки B до плоскости. Так как точка D - проекция точки B на плоскость ABCA1B1C1, то она будет лежать на высоте треугольника ABC. А так как треугольник ABC равносторонний, то все его высоты будут равны 0.866.

Таким образом, расстояние от точки B до плоскости будет равно расстоянию от точки D до центра основания треугольной призмы. Это расстояние можно найти с помощью теоремы Пифагора. Так как точка D делит высоту треугольника ABC пополам, то получаем, что расстояние от точки D до центра основания треугольной призмы равно 0.866 / 2 = 0.433.

Итак, расстояние от точки B до плоскости ABCA1B1C1 равно 0.433 единицы длины.