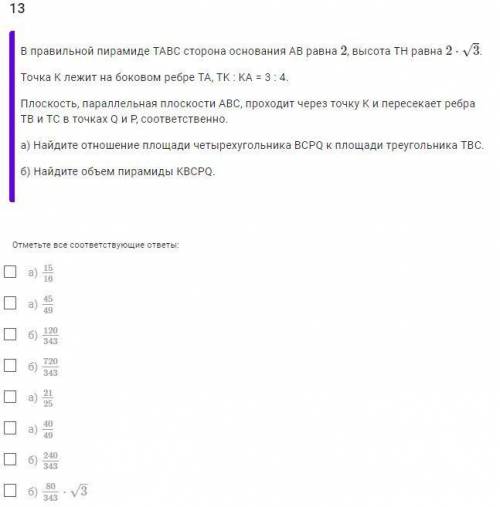
В правильной пирамиде TABC сторона основания AB равна 2, высота TH равна 2⋅√3. Точка K лежит на боковом ребре TA, TK : KA = 3 : 4. Плоскость, параллельная плоскости ABC, проходит через точку K и пересекает ребра TB и TC в точках Q и P, соответственно.
а) Найдите отношение площади четырехугольника BCPQ к площади треугольника TBC.
б) Найдите объем пирамиды KBCPQ.

Добрый день! Давайте решим данный вопрос.

а) Найдем отношение площади четырехугольника BCPQ к площади треугольника TBC.
Поскольку пирамида TABC является правильной, то треугольник TBC является равносторонним. Значит, все его стороны равны.

Так как AB = 2, то BC = AB = 2.
При этом, поскольку треугольник TBC -- равносторонний, то TB = BC = 2.

Так же, по условию, точка K лежит на боковом ребре TA, и отношение TK : KA равно 3 : 4.
Из этого можно сделать вывод, что TK = (3 / 7) * TA и KA = (4 / 7) * TA.

Очевидно, что площадь треугольника TBC равна (TB * BH) / 2, где BH -- высота, опущенная из вершины T на основание BC.
Так как треугольник TBC равносторонний, то его высота BH -- это половина стороны BC, то есть BH = BC / 2 = 1.

Теперь мы знаем, что высота TH равна 2 * √3 и, следовательно, TA = TH / √3 = 2 * √3 / √3 = 2.
Тогда TK = (3 / 7) * 2 = 6 / 7 и KA = (4 / 7) * 2 = 8 / 7.

Поскольку плоскость, параллельная плоскости ABC, проходит через точку K и пересекает ребра TB и TC в точках Q и P соответственно, то треугольник TBQ подобен треугольнику TBC по двум сторонам. Следовательно, их соответствующие стороны пропорциональны: BQ : BC = TK : TA.

Заметим, что BQ = BC - CQ, а TC - TP = PC. Тогда выражение BQ : BC преобразуется: (BC - CQ) / BC = 1 - CQ / BC.
Так как треугольник TBC равносторонний, то BC = 2. Подставим это значение в выражение: 1 - CQ / 2.

Следовательно, альтернативная пропорция выглядит следующим образом: 1 - CQ / 2 = (6 / 7) / 2.
Решим эту пропорцию:

1 - CQ / 2 = (6 / 7) / 2
(2 / 2) - CQ / 2 = 6 / (7 * 2) // Сокращаем дробь в правой части на общий множитель 2
1 - CQ / 2 = 6 / 14
1 - CQ / 2 = 3 / 7 // Теперь домножим обе части на 2, чтобы избавиться от знаменателя
2 - CQ = 6 / 7
-CQ = 6 / 7 - 2
-CQ = (6 - 14) / 7
-CQ = -8 / 7
CQ = 8 / 7

Теперь, когда мы знаем CQ, мы можем найти BQ = BC - CQ = 2 - 8 / 7 = (14 - 8) / 7 = 6 / 7.

Аналогичным образом, применяя пропорции, мы можем найти PQ = (8 * TC) / TA и TP = (8 * TB) / TA.

PQ = (8 * TC) / TA = (8 * 2) / 2 = 8.
TP = (8 * TB) / TA = (8 * 2) / 2 = 8.

Теперь мы можем вычислить площадь четырехугольника BCPQ.
Обратимся к формуле площади трапеции: S = (a + b) * h / 2, где a и b - длины параллельных сторон, h - высота трапеции.

В нашем случае, a = BC = 2, b = PQ = 8, а h - это перпендикуляр, проведенный к основаниям BQ и PC из точки P.
Так как и BQ, и PC уже известны, h = TP = 8.

Тогда площадь четырехугольника BCPQ будет равна S = (a + b) * h / 2 = (2 + 8) * 8 / 2 = 10 * 8 / 2 = 40.

Теперь найдем площадь треугольника TBC. Мы уже знаем, что это равносторонний треугольник, поэтому его площадь будет равна (TB * BH) / 2 = (2 * 1) / 2 = 1.

Таким образом, отношение площади четырехугольника BCPQ к площади треугольника TBC равно 40 / 1 = 40.

б) Теперь найдем объем пирамиды KBCPQ.
Формула для объема пирамиды V = (S * h) / 3, где S - площадь основания пирамиды, h - высота пирамиды.

Мы уже вычислили площадь четырехугольника BCPQ, которая составляет 40.

Высоту пирамиды KBCPQ можно найти, применяя теорему Пифагора для прямоугольного треугольника TKH:
TH^2 = TK^2 + KH^2. Поскольку TH = 2 * √3, TK = 6/7, найдем KH.

TK^2 + KH^2 = TH^2
(6/7)^2 + KH^2 = (2 * √3)^2
(36/49) + KH^2 = 12
KH^2 = 12 - 36/49
KH^2 = (588 - 36) / 49
KH^2 = 552 / 49
KH = √(552 / 49)

Таким образом, данная выражение является высотой пирамиды KBCPQ.

Теперь можем вычислить объем пирамиды KBCPQ: V = (S * h) / 3 = (40 * √(552 / 49)) / 3.

Оставляем ответ в таком виде, поскольку невозможно выразить корень точно.