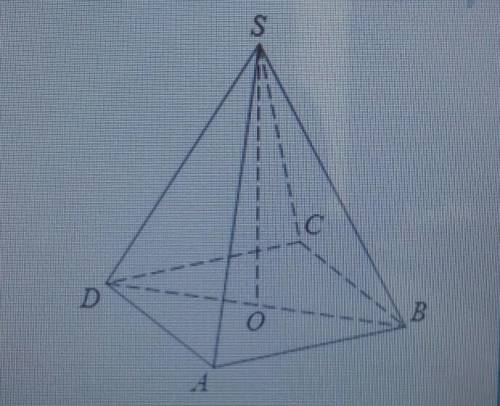
В правильной четырёхугольной пирамиде SABCD точка О-центр основания, S-вершина, SD=10, SO=6. Найдите длину отрезка АС.
Другие вопросы по теме Геометрия
Популярные вопросы
- Разбор слова по составу дарил , жалел . сразу большое...
2 - Лит-ра 10 класс в инете ничего нет. кто что знает пишите. 1)неповторимый...
3 - Если у трехзначного числа стереть стоящую слева единицу, то оно уменьшится...
1 - Врастительном покрове лесостепей : а-мелколиственные породы деревьев...
2 - Напишите 10 предложений про пословицу не откусывай больше того, что...
2 - Составить предложения с фразеологизмом вывести из себя...
2 - Выражения: 4(2+х)-3(1+х); 11(5с+d)+3(d+c) желательно по подробнее...
2 - Назовите причины следующих явлений: а) уровень смертности в развивающихся...
3 - Мне сделать синтаксический разбор предложения: подкрался я к ним...
1 - Превратит текст рассуждение в текст описание: зебра-дикая лошадь....
2
В данном случае, мы имеем пирамиду SABCD, где S - вершина пирамиды, AB, BC, CD, DA - стороны её основания, а D - центр основания. Отрезок SO представляет высоту пирамиды.
Посмотрим на треугольник SOD, образованный вершиной пирамиды S, центром основания D и точкой О (центр). Так как OD - это радиус основания, то OD = CD/2.
В данной задаче говорится, что CD = 10, поэтому OD = 10/2 = 5.
Также, из условия задачи мы знаем, что SO = 6. Теперь мы можем рассмотреть треугольник SDO, в котором известны две стороны (OD и SO) и мы хотим найти третью сторону SD.
Теперь мы можем использовать теорему Пифагора для треугольника SDO:
SD^2 = SO^2 + OD^2
Подставляем известные значения:
SD^2 = 6^2 + 5^2
SD^2 = 36 + 25
SD^2 = 61
Чтобы найти длину отрезка SD, нам нужно извлечь квадратный корень из 61:
SD = sqrt(61)
Теперь, чтобы найти длину отрезка AC, мы можем рассмотреть треугольник ACD. Он является прямоугольным треугольником с гипотенузой AC, сторонами AD и CD. Мы знаем, что AD = CD = 10 (так как это стороны основания пирамиды).
Теперь мы можем использовать теорему Пифагора для треугольника ACD:
AC^2 = AD^2 + CD^2
Подставляем известные значения:
AC^2 = 10^2 + 10^2
AC^2 = 100 + 100
AC^2 = 200
Чтобы найти длину отрезка AC, нам нужно извлечь квадратный корень из 200:
AC = sqrt(200)
Однако, мы можем упростить этот ответ. 200 можно разложить на множители: 200 = 2 * 2 * 2 * 5 * 5 = 2^3 * 5^2. Извлекаем корень из каждого множителя и получаем:
AC = sqrt(2^3 * 5^2) = 2 * 5 * sqrt(2) = 10 * sqrt(2)
Таким образом, длина отрезка AC равна 10 * sqrt(2).