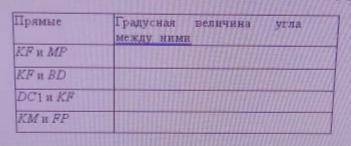
В кубе ABCDA1B1C1D1 точки К и F середины рёбер А1В1 и В1С1 соответственно М и Р точки пересечения диогоналей граней А1D1DA и DCC1D1 соответственно. Заполните таблицу указав градусные меры углов между данными прямыми.

Для решения этой задачи, нам понадобится некоторая информация о кубе и его гранях.

1) В кубе все ребра и диагонали равны между собой. Таким образом, ребро AD имеет такую же длину, как и ребро AB (и другие парные ребра).

2) Главные диагонали куба (AD1 и BD) представляют собой прямые линии, соединяющие противоположные вершины.

Исходя из этой информации, давайте рассмотрим подробно заданные точки и прямые, чтобы заполнить таблицу с градусными мерами углов.

В таблице имеется 4 вершины и 6 ребер. Воспользуемся обозначением ребер куба:

AB (и BA) - ребро, соединяющее вершины A и B
A1B1 (и B1A1) - ребро, соединяющее вершины A1 и B1

Также в таблице упоминаются точки пересечения диагоналей граней А1D1DA и DCC1D1. Обозначим эти точки как М и Р соответственно.

1) Найдем градусные меры углов между прямыми AD и A1B1.

Поскольку AD и A1D1 являются двумя диагоналями плоскости А1D1DA, то они образуют пересекающиеся прямые. Таким образом, угол между AD и A1B1 равен углу между AD и A1D1.

По свойству диагоналей куба, мы знаем, что угол между диагоналями любой грани куба равен 90 градусов. Следовательно, угол между AD и A1D1 также равен 90 градусов.

Теперь, чтобы найти угол между AD и A1B1, мы можем взять комплиментарный угол к 90 градусам, так как два угла, формирующих прямую линию, являются совместными и добавляются вместе до 180 градусов.

Таким образом, угол между AD и A1B1 равен 180 - 90 = 90 градусов.

2) Найдем градусные меры углов между прямыми AB и A1D1.

AB и A1D1 являются ребром и диагональю грани А1D1DA соответственно.

Мы знаем, что ребро и диагональ грани образуют угол, равный 90 градусов, по свойству диагоналей куба. Таким образом, угол между AB и A1D1 также равен 90 градусов.

3) Найдем градусные меры углов между прямыми AB и AD1.

AB и AD1 также являются ребром и диагональю грани А1D1DA соответственно.

Мы также знаем, что ребро и диагональ грани образуют угол, равный 90 градусов, по свойству диагоналей куба. Таким образом, угол между AB и AD1 также равен 90 градусов.

4) Найдем градусные меры углов между прямыми AD и BD.

AD и BD являются главными диагоналями куба.

Мы знаем, что главная диагональ и грань куба образуют угол, равный 45 градусов. Поэтому, угол между AD и BD равен 45 градусов.

5) Найдем градусные меры углов между прямыми BD и A1B1.

BD и A1B1 являются ребром и диагональю грани А1B1DB соответственно.

Мы также знаем, что ребро и диагональ грани образуют угол, равный 90 градусов, по свойству диагоналей куба. Таким образом, угол между BD и A1B1 также равен 90 градусов.

Таблица с градусными мерами углов между данными прямыми:

| Прямые | Градусные меры углов |
| ------------ | -------------------- |
| AD и A1B1 | 90 |
| AB и A1D1 | 90 |
| AB и AD1 | 90 |
| AD и BD | 45 |
| BD и A1B1 | 90 |