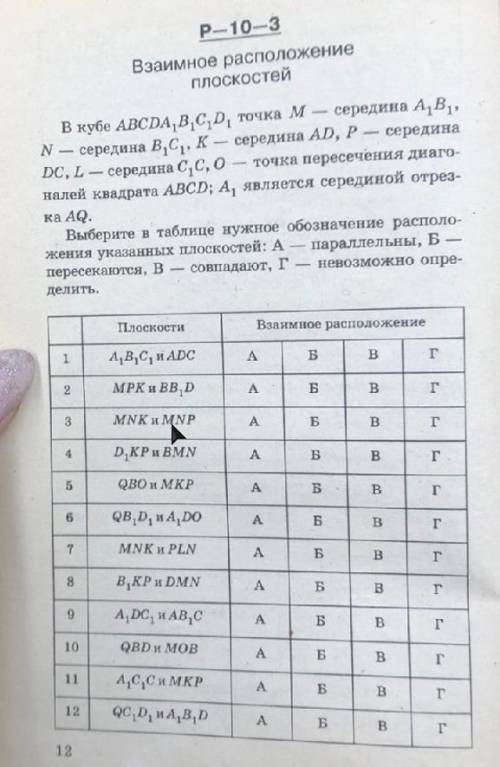
В кубе ABCDA1B1C1D1 точка M - середина A1B1, N - середина B1C1, K - середина AD, P - середина DC, L - середина C1 C,O - точка пересечения диагоналей квадрата ABCD; A1 является серединой отрезка AQ Выберите в таблице нужное обозначение расположения указанных плоскостей: A - параллельны, Б - пересекаются, В - совпадают, г - невозможно определить

Давай разберемся с расположением указанных плоскостей в данном кубе.

1. Плоскость, проходящая через точки B, C1, M и N:
Для начала построим отрезок B1M и отрезок CN. Затем проведем прямую через эти две точки. Видим, что эта прямая пересекает плоскость ABCD в точках B и C1, а также проходит через точки M и N. Следовательно, данная плоскость пересекает плоскость ABCD. Ответ: Б.

2. Плоскость, проходящая через точки A, L, P и D1:
Аналогично построим отрезок LP и отрезок AD1. Затем проведем прямую через эти две точки. Видим, что эта прямая пересекает плоскость ABCD в точках A и D1, а также проходит через точки L и P. Следовательно, данная плоскость пересекает плоскость ABCD. Ответ: Б.

3. Плоскость, проходящая через точки A, M, O и Q:
Точка O является точкой пересечения диагоналей квадрата ABCD. Значит, данная плоскость проходит через точки A и O, которые уже находятся в плоскости ABCD. Остается проверить, проходят ли точки M и Q также в этой плоскости. Построим отрезок MQ. Заметим, что этот отрезок лежит в плоскости ABCD, так как все его точки также лежат на ребре A1B1, которое лежит в плоскости ABCD. Следовательно, данная плоскость совпадает с плоскостью ABCD. Ответ: В.

4. Плоскость, проходящая через точки B, K, O и C1:
Точка O является точкой пересечения диагоналей квадрата ABCD. Построим отрезок BK. Заметим, что этот отрезок лежит в плоскости ABCD, так как все его точки также лежат на ребре AD, которое лежит в плоскости ABCD. Проведем прямую через точки K и B. Видим, что эта прямая пересекает плоскость ABCD в точках B и K, а также проходит через точки O и C1. Следовательно, данная плоскость пересекает плоскость ABCD. Ответ: Б.

5. Плоскость, проходящая через точки M, N, L и P:
Построим отрезок MN и отрезок LP. Заметим, что эти два отрезка пересекаются в точке O, которая является точкой пересечения диагоналей квадрата ABCD. Следовательно, все точки M, N, L и P лежат в одной плоскости, которая проходит через точку O. Ответ: Б.

Таким образом, расположение указанных плоскостей в данном кубе можно обозначить следующим образом:
1. Плоскость, проходящая через точки B, C1, M и N: Б (пересекается).
2. Плоскость, проходящая через точки A, L, P и D1: Б (пересекается).
3. Плоскость, проходящая через точки A, M, O и Q: В (совпадает).
4. Плоскость, проходящая через точки B, K, O и C1: Б (пересекается).
5. Плоскость, проходящая через точки M, N, L и P: Б (пересекается).