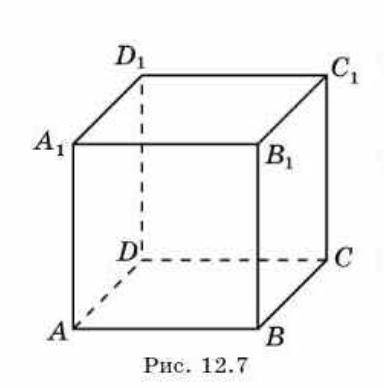
В единичном кубе abcda1b1c1d1 найдите расстояние от вершины А до плоскости a) ВСС1 b) BCD1

a) 1 ; b)√2/2

Объяснение:

Так как длина ребра куба 1, а расстояние это перпендикуляр, то расстояние от точки A до плоскости BCC1, будет ребро AB длиной 1,во втором случае диагональ A1B принадлежит плоскости BCD1, в этом случае легче будет рассмотреть квадрат AA1B1B, так как по свойству квадрата его диагонали точкой пересечения деляться на 2, и пересекаются под прямым углом, то половина диагонали AB1 будет расстоянием от точки до плоскости. Если где-то неправ сообщите об этом в комментарии.