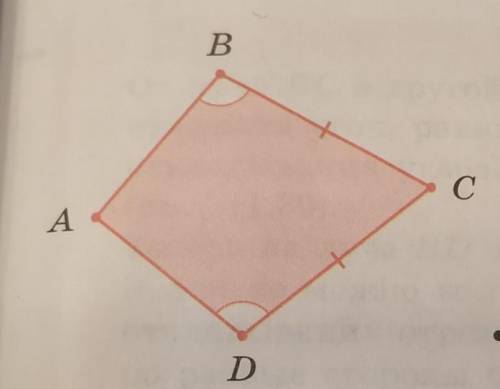
В четырёхугольнике ABCD угол АВС
равен углу ADC, BC = CD. Докажите, что его диагонали перпендикулярны друг другу
​

Доказательство:

В данном вопросе мы должны доказать, что диагонали четырёхугольника ABCD перпендикулярны друг другу.

Для начала, обратим внимание на условие задачи: угол АВС равен углу ADC, а также BC = CD. Для упрощения обозначений, заменим углы на их меру в градусах: угол АВС = угол ADC = α, а стороны от углов обозначим как a, b и c (AB, BC и CD соответственно).

1. Рассмотрим треугольник ABC:
- Так как BC = CD, то сторона BC равна стороне CD.
- Угол ABC равен углу ACD, так как это (по условию) один и тот же угол.
- Угол BAC равен углу CDA, так как они дополняются друг другу (сумма углов в треугольнике равна 180 градусам).
Из этих сведений следует, что треугольник ABC равен треугольнику CDA по стороне-стороне-стороне (ССС).

2. Поскольку треугольник ABC равен треугольнику CDA по ССС, то соответствующие углы этих треугольников должны быть равными. Исходя из этого, угол CAB равен углу CDA (обозначим их оба как β).
- Также, угол ABC равен углу ACD (обозначим их оба как γ).

3. Из треугольника ABC:
- Угол CAB равен углу CBA (так как имеет две равные стороны и равная основа).
- Угол ABC равен углу BAC (так как они дополняются друг другу).
- Углы CAB, ABC и BAC обозначены выше как β.
Таким образом, получаем, что у треугольника ABC все углы равны β.

4. Из треугольника CDA:
- Угол CAD равен углу CDA (так как имеет две равные стороны и равная основа).
- Угол CDA равен углу DAC (так как они дополняются друг другу).
- Углы CAD, CDA и DAC обозначены выше как гамма.
Таким образом, получаем, что у треугольника CDA все углы равны гамма.

5. Из пунктов 3 и 4 получаем, что углы CAB, ABC и BAC равны β, а углы CAD, CDA и DAC равны гамма.

6. Поскольку углы CAB и CAD измеряются α, а углы ABC и CDA измеряются β, получаем, что α = β = γ.

7. Таким образом, получаем, что углы CAB, ABC и BAC равны γ, что означает, что треугольник ABC - равносторонний.

8. Из пункта 7, сторона AC в треугольнике ABC равна стороне AD в треугольнике ACD.

9. В четырёхугольнике ABCD проведём обе диагонали AC и BD.

10. Поскольку углы CAB и BAD измеряются γ, а углы ABC и ABD измеряются γ, и сторона AC равна стороне AD (см. пункт 8), получаем, что треугольники CAB и BAD равны по стороне-стороне-стороне (ССС).

11. Из пункта 10 следует, что углы ACB и ADB равны и ображют прямой угол (180 градусов).

12. Так как углы ACB и ADB равны и образуют прямой угол, а диагонали CD и AB соответствуют этим углам, получаем, что диагонали CD и AB перпендикулярны друг другу.

Таким образом, мы доказали, что в четырёхугольнике ABCD диагонали CD и AB перпендикулярны друг другу, используя равенство углов и равность сторон треугольников ABC и ACD.