В ΔABC ∠C - тупой, а точка D выбрана на продолжении AB через точку B так, что ∠ACD = 135°. Точка D' симметрична D относительно BC. Точка D'' симметрична D' относительно АС и лежит на BC. Известно, что CD'' = 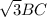 ; AC = 6. Доказать, что ΔCBD - равнобедренный.
; AC = 6. Доказать, что ΔCBD - равнобедренный.
Другие вопросы по теме Геометрия
Популярные вопросы
- Врулоне синей ткани было в 1,5 раза больше, чем в рулонекрасной ткани. сколько...
3 - Какое слово прощание дескать,значит,итак или таким образом?...
1 - 1.усi слiд писати з и в рядкуа. л(и,е)сточок, ш(и,е)потiти, т(и,е)хенько. б. ар(и,е)штантський,...
2 - Петр i - самый полный тип эпохи или призванный к жизни гений-палач, для которого...
2 - Две хорды пересекаются внутри круга. одна из хорд делится на отрезки, равные 24...
1 - Точка d симетрична точці m(7; -5) відносно осі абсцис. знайдіть координати точки...
1 - Имя прилогательное это часть речи которая обозначает...
3 - определить, какие значения x, y, z будут выведены после выполнения фрагмента программы...
3 - Исправьте ошибки в тексте: отец последнее время часто дома контора теперь редко...
2 - Рассказ начинается так: много лет над лесом дуб высится скиньте продолжение текста....
1
СD=CD'
Δ СPD' = Δ CPD'' по построению симметричной точки D''⇒
СD'=CD''
СD = CD' = CD''
BС – серединный перпендикуляр к DD' ⇒
BD=BD'
Обозначим
∠ СD'D= ∠ CDD'= α
∠ CD'D'' = ∠ CD''D'= β
Проведем DK ⊥ AC;
DK || D'D''
Δ CDK – прямоугольный равнобедренный треугольник.
∠CDK =∠ KСD=45o
PD'DK – прямоугольная трапеция.
Cумма углов, прилежащих к стороне DD' равна 180o
∠CDK +∠ СDD'+ ∠ DD'C+ ∠ CD'D'' =180o ⇒
45o+ α + α + β =180o ⇒
2 α + β =135o
В прямоугольном треугольнике MD'D''
сумма острых углов равна 90 o
∠ DD'C+ ∠ CD'D'' + ∠ CD''D' =90o ⇒
α + β+β =90o
Решаем систему двух уравнений:
{2 α + β =135o
{α + 2β =90o
Умножаем первое уравнение на 2:
{4α + 2β =270o
{α + 2β =90o
Вычитаем из первого второе
3α=180o
α =60o
Δ СDD' – равносторонний.
BD=BD' ⇒ B – равноудалена от двух вершин равностороннего треугольника, значит равноудалена и от третьей.
BD=BD'=ВС
BD=BC и значит Δ СBD – равнобедренный, что и требовалось доказать.