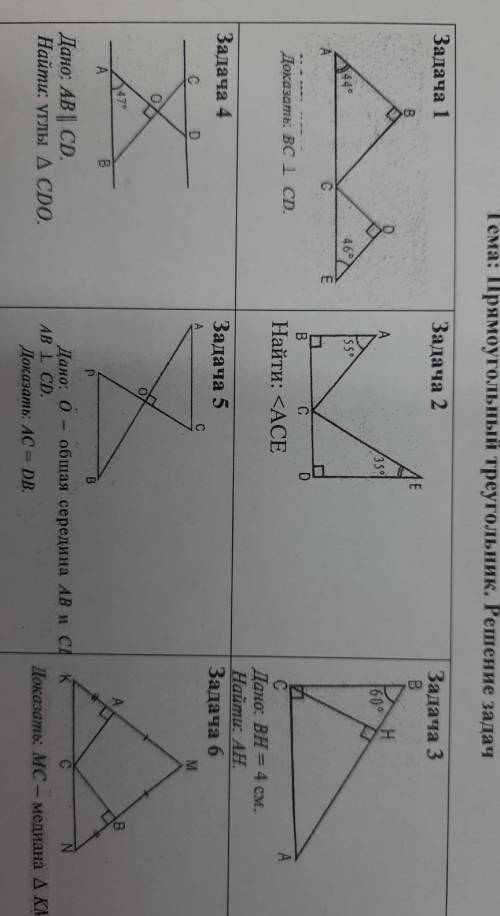
Умоляю решите 2;3;4 задачи большое заранее)
Другие вопросы по теме Геометрия
Популярные вопросы
- Сформувати основні товари на продаж та провести АВС – аналіз, якщо Ви здійснюєте...
1 - Сума двох чисел дорівнює 80,а їх добуток дорівнює 1200 знйти всі числа...
1 - Увертюра – фантазия «Ромео и Джульетта» — одно их самых знаменитых произведений...
2 - ответь на во о взаимодействии металлов с химическими соединениями. Какой из данных...
2 - У большинства земноводных:один круг кровообращенияжаберное дыханиекожно-лёгочное...
3 - Сравните два образа что общего у яркого мака и алексея сына ольги...
3 - Инвестиционный фонд объявил, что доходность по месячным вложениям в него превышает...
3 - Portfolio Use the ideas from the dialogue in Ex. 3 tocomplete the email below,...
1 - Описати діяльність К. Розумовського...
1 - Обчислити кут С трикутника АВС, якщо A (1; 3; -2), В (2; 0; 1), C (3; -4; 0)....
3
ответ: 90°; 12 см; ∠COD=90°; ∠ОСD=43°; ∠ОDС=47°
Объяснение: 2) треугольники АВС и СDE прямоугольные ∠АСВ=90-55=35°.
∠ECD=90-35=55°
∠АСЕ развернутый и равен 180°
Значит ∠АСЕ=∠ВСD-∠ЕСD-∠АСВ=180-35-55=90°
3) ∠СВH=60°. Значит ∠ВСH=90-60=30°
BH лежит против угла 30° и является катетом ΔСBH. ВС гипотенуза в это треугольнике. Значит ВС=ВH*2=4*2=8 cм.
∠САВ тоже 30° и СВ летит против угла 30°. Значит АС=ВС*2=8*2=16 см. АH=АВ-ВH=16-4=12 cм
4) ∠ВАО=∠СD0=47°, как накрест лежащие при пересечении параллельных прямых секущей.
∠АОВ=∠СОD=90°, как вертикальных углы.
Значит ∠АВО=∠ОСD=90-47=43°