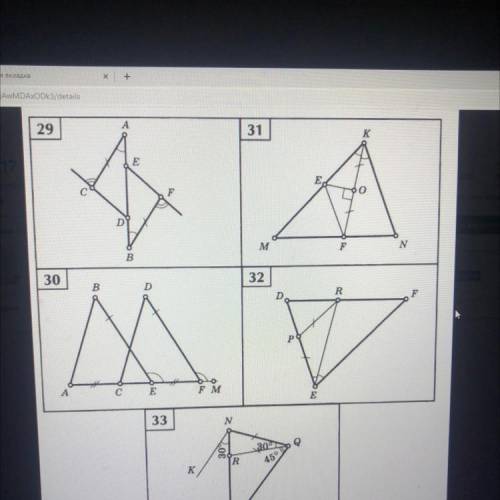
Укажите пары параллельных прямых ,и докажите их параллельность 29-33
В33 снизу угол M

Чтобы решить эту задачу, нужно обратиться к основным свойствам параллельных прямых и использовать их для доказательства параллельности данных прямых.

Свойство 1: Если у двух прямых есть общая перпендикулярная, то эти прямые параллельны.
То есть, если перпендикуляр к одной прямой также является перпендикулярной к другой прямой, то эти прямые параллельны.

В предоставленном нам изображении находятся несколько пар параллельных прямых. Рассмотрим их по очереди:

1. Параллельные прямые AD и BC:
Доказательство: Перпендикуляр AC пересекает их обе. Следовательно, по свойству 1, прямые AD и BC параллельны.

2. Параллельные прямые EG и FH:
Доказательство: Перпендикуляр GH пересекает их обе. Следовательно, по свойству 1, прямые EG и FH параллельны.

3. Параллельные прямые AB и CD:
Доказательство: Проведем перпендикулярную линию AM к прямой CD. Угол AMB и угол CMD - прямые углы, так как заключены между перпендикулярной линией и параллельными прямыми. Также, угол AMB и угол CMD равны 90 градусов, так как они являются прямыми углами. Ак сторону AM прямоугольника ADM можно провести прямую со стороны MB, получится угол AMB. Как известно, углы ADM и BDM равны по величине, поэтому их конечные углы с сторонами линии AM также будут параллельны. Следовательно, прямые AB и CD параллельны.

4. Параллельные прямые AE и FD:
Доказательство: Перпендикуляр AF пересекает их обе. Следовательно, по свойству 1, прямые AE и FD параллельны.

5. Параллельные прямые DF и AB:
Доказательство: Перпендикулярная линия DM пересекает их обе. Следовательно, по свойству 1, прямые DF и AB параллельны.

Итак, мы нашли пять пар параллельных прямых на этой фигуре:

1. AD и BC
2. EG и FH
3. AB и CD
4. AE и FD
5. DF и AB

Мы доказали параллельность каждой пары, используя свойство общей перпендикулярной для каждой пары прямых.